Числовые характеристики случайных величин. Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности.

Пусть случайная величина Х может принимать только значения 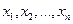, вероятности которых соответственно равны 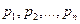. Тогда математическое ожидание M(X) случайной величины определяется равенством

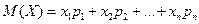(5)

Если дискретная случайная величина Х принимает счётное множество возможных значений, то

, (6)

причём математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг её среднего значения (математического ожидания).

Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

(7)

Дисперсия характеризует разброс значений случайной величины Х относительно её математического ожидания. Из определения дисперсии следует формула для её вычисления:

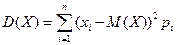(8)

Иногда удобно применить формулу:

(9)

т.е. дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом её математического ожидания.

Для оценки рассеяния возможных значений случайной величины вокруг её среднего значения кроме дисперсии может использоваться и среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии:

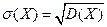(10)