Циркуляция вектора для магнитного поля в вакууме
Циркуляция вектора 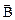 по заданному замкнутому контуру
по заданному замкнутому контуру 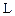 – это интеграл вида:
– это интеграл вида: 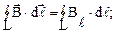
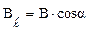 .
.
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора 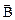 )
) 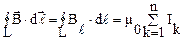 , где
, где
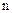 – число проводников с током, охватываемых контуром
– число проводников с током, охватываемых контуром 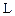 .
.
Циркуляция вектора 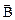 по произвольному замкнутому контуру
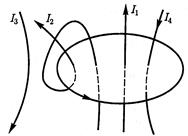
по произвольному замкнутому контуру 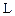 равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта (рисунок 14).
равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта (рисунок 14).
|
Пример:
|
Поле, в котором циркуляция вектора 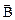 не равна 0, называется вихревым. Магнитное поле является вихревым.
не равна 0, называется вихревым. Магнитное поле является вихревым.
|
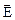 ).
).
Дата добавления: 2015-06-12; просмотров: 753;

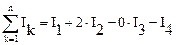 .
.