Вращение плоскости поляризации. Многие вещества, называемые оптически активными, обладают способностью поворачивать плоскость поляризации.

Многие вещества, называемые оптически активными, обладают способностью поворачивать плоскость поляризации.

Это кристаллические тела (кварц и др.), чистые жидкости (скипидар и др.) и растворы оптически активных веществ (например, водный раствор сахара).

,

где d – расстояние, пройденное светом в оптически активном веществе; с – концентрация раствора; α ([α]) – удельное вращение (или постоянная вращения). Постоянная α имеет различное значение для разных веществ и, кроме того, сильно зависит от длины волны света. Так для кварцевой пластинки толщиной 1 мм углы поворота желтого и фиолетового света равны соответственно 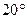и .

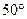В зависимости от направления вращения плоскости поляризации, оптически активные вещества подразделяют на право и левовращающие, то есть вращающие по или против часовой стрелки, если смотреть навстречу световому пучку.

Вращательная способность кварца связана с особенностями кристаллической структуры, расположением частиц в кристаллической решетке (на макроуровне), так как плавленый кварц не обладает оптической активностью.

Измерение угла поворота плоскости поляризации используется для определения концентрации оптически активных веществ, например сахара в растворах (пищевая промышленность) и биологических объектах (кровь).

Отметим, что способность поворачивать плоскость поляризации приобретают даже оптически неактивные вещества, если их поместить в магнитное поле (эффект Фарадея).

Вопросы для самоконтроля.

1. Чем отличается поляризованный свет от естественного? Каковы виды поляризованного света?

2. В чем смысл закона Брюстера?

3. В чем суть двойного лучепреломления? В чем особенности обыкновенного и необыкновенного лучей? Как объяснить двойное лучепреломление?

4. Что такое оптическая ось кристалла?

5. Объясните закон Малюса для света, прошедшего через два поляризатора.

6. Объясните эффект Керра.

7. С чем связано вращение плоскости поляризации на макро- и микроуровнях? Где применяется?

Лекция № 35