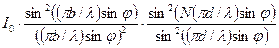Дифракция Френеля на круглом непрозрачном диске.
 |
Однако даже если m достаточно велико, то амплитуда колебаний в т. Р всегда отлична от нуля, т. е. центр геометрической тени диска всегда будет освещен! При любом m наблюдается пятно – «пятно Пуассона». С увеличением радиуса диска интенсивность центрального максимума падает, так как уменьшается 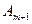 .
.
2. Дифракция Фраунгофера на одной щели.
Пусть плоская волна падает нормально на непрозрачный экран, в котором имеется бесконечно длинная узкая щель шириной b. Когда фронт волны дойдет до щели, то все ее точки станут, согласно принципу Гюйгенса-Френеля источниками вторичных когерентных волн (рис. 33.4).
 | |||
 | |||
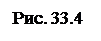
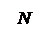

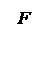
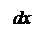
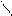
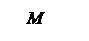
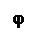
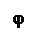
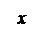
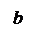


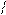













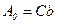 , отсюда
, отсюда 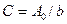 (угол φ - между нормалью к щели и некоторым произвольным направлением волны после щели). Тогда световое возмущение (колебание) в элементе dx dξ =
(угол φ - между нормалью к щели и некоторым произвольным направлением волны после щели). Тогда световое возмущение (колебание) в элементе dx dξ = 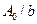 cosωt.
cosωt.
Распространение колебаний в пространстве это волна. В точку N волна от dx (т. M) приходит с запаздыванием по ходу по сравнению с волной от т. F (где фаза ωt как и в т. M с координатой x) в направлении φ MN = xsinφ.
Световая волна в т. N
dξ = 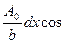 (ωt – кхsinφ), где к = 2π /λ – волновое число.
(ωt – кхsinφ), где к = 2π /λ – волновое число.
Результирующая световая волна от всех точек щели в направлении угла φ получается интегрированием по ширине щели
ξ = 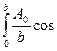 (ωt – кхsinφ)dx.
(ωt – кхsinφ)dx.
Введем под знак дифференциала (ωt – кхsinφ) и, соответственно, чтобы не изменился результат, разделим на (– кхsinφ).
ξ = 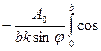 (ωt – кхsinφ)d(ωt – кхsinφ) =
(ωt – кхsinφ)d(ωt – кхsinφ) = 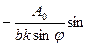 (ωt – кхsinφ)
(ωt – кхsinφ) 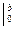 =
=
= 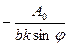 [sin(ωt – кхsinφ) – sin(ωt)].
[sin(ωt – кхsinφ) – sin(ωt)].
Воспользуемся формулой разности синусов
( 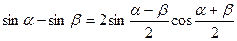 ), тогда
), тогда
ξ = 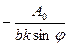 2
2 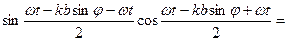
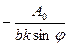
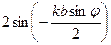 ∙
∙
∙ 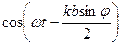 .
.
 Подставляя вместо k его значение 2π /λ, учтем, что функция sin нечетная, получим
Подставляя вместо k его значение 2π /λ, учтем, что функция sin нечетная, получим
 ξ =
ξ = 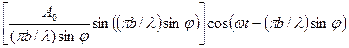
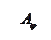
Амплитуда световой волны, идущей в направлении φ
 |
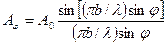
Поскольку интенсивность пропорциональна квадрату амплитуды, то интенсивность света под углом φ
|
(33-3)
где 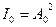 .
.
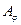 (соответственно
(соответственно 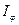 ) обращается в нуль для углов
) обращается в нуль для углов 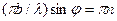
|
(где n = 1, 2, 3…), то есть для , или
|
(33-4)
Получим условие минимумов интенсивности для дифракции на щели (33-4).

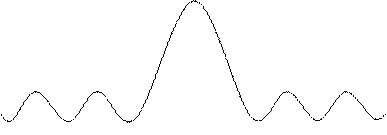
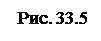 Картина распределения интенсивности световой волны
Картина распределения интенсивности световой волны 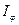 в зависимости
в зависимости 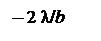

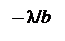
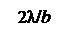
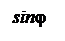
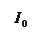
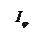




















 3. Дифракция Фраунгофера на одномерной дифракционной решетке. Дифракционная решетка представляет ряд параллельных щелей
3. Дифракция Фраунгофера на одномерной дифракционной решетке. Дифракционная решетка представляет ряд параллельных щелей
 |



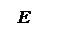










 внимание их взаимную интерференцию (многолучевая интерференция).
внимание их взаимную интерференцию (многолучевая интерференция).
 |
Δ = СЕ = dsinφ (из прямоугольного треугольника АСЕ). И если
|
 где m = 0, 1, 2, …, то лучи, идущие от аналогичных точек соседних щелей
где m = 0, 1, 2, …, то лучи, идущие от аналогичных точек соседних щелей
 | |||
 | |||


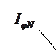 | |||||
 | |||||
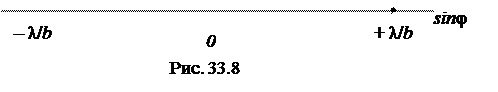 |
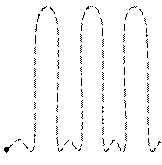
приходить в одной фазе и усиливать друг друга. В направлении φ, удовлетворяющему условию (33-4), будут так называемые главные максимумы интенсивности (рис. 33.8). Очевидно, что минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (33-3) (условие ми-
 |
нимумов для одной щели 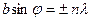 (n = 1, 2, 3…) (главные минимумы).
(n = 1, 2, 3…) (главные минимумы).
Отметим, что кроме главных минимумов имеются дополнительные минимумы из условия dsinφ = 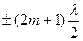 (m = 0, 1, 2…). Количество этих минимумов зависит от количества щелей в дифракционной решетке (для двух щелей – один, для трех – два и т. д.). Так как модуль sinφ не может быть больше единицы, то из условия (33-5) следует, что число главных максимумов m
(m = 0, 1, 2…). Количество этих минимумов зависит от количества щелей в дифракционной решетке (для двух щелей – один, для трех – два и т. д.). Так как модуль sinφ не может быть больше единицы, то из условия (33-5) следует, что число главных максимумов m 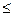 d/λ.
d/λ.
Распределение интенсивности света на экране за дифракционной решеткой 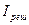 (без вывода):
(без вывода):
|
(33-5)
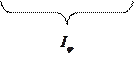 | 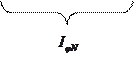 | ||
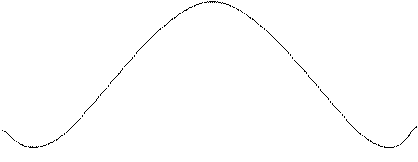
Согласно выражению (33-5) распределение интенсивности при дифракции на решетке определяется произведением двух функций 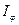 - распределение интенсивности (33-3) при дифракции на одной щели (на рис. 33.8 - сплошная линия) и многолучевой интерференции световых волн от всех щелей дифракционной решетки
- распределение интенсивности (33-3) при дифракции на одной щели (на рис. 33.8 - сплошная линия) и многолучевой интерференции световых волн от всех щелей дифракционной решетки 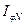 . В результате получается распределение
. В результате получается распределение 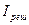 в виде жирной линии на рис 33.8 (кривая интенсивности на щели как бы «зарезает» максимумы
в виде жирной линии на рис 33.8 (кривая интенсивности на щели как бы «зарезает» максимумы 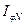 ). Дополнительные минимумы, их количество, изображены условно.
). Дополнительные минимумы, их количество, изображены условно.
Отметим важный момент. Положение главных минимумов зависит от длины волны λ (см. (33-5)). Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр. Это свойство дифракционной решетки используется для исследования спектрального состава света (определение длин волн и интенсивностей его компонентов) т. е. дифракционная решетка может быть использована как спектральный прибор.
Разрешающая сила дифракционной решетки R = λ /Δλ; где Δλ - минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются отдельно. В более подробных курсах показывается, что R = mN, где m – порядок спектра, N – число штрихов на дифракционной решетке. (Примечание: кроме прозрачных дифракционных решеток имеются непрозрачные – отражательные, на которых имеются продольные штрихи (аналог непрозрачной части), промежутки между штрихами отражают свет и являются аналогами прозрачных частей (щелей)).
4. Понятие голографии (от греч. голос – весь, графо – пишу).























 Голография – это способ записи волнового поля и его последующего восстановления, основанный на регистрации интерференционной картины. Изобретен англ. физиком Д. Габором в 1947 году. (Нобелевская премия 1971 г.)
Голография – это способ записи волнового поля и его последующего восстановления, основанный на регистрации интерференционной картины. Изобретен англ. физиком Д. Габором в 1947 году. (Нобелевская премия 1971 г.)
 | |||||
 | |||||
 | |||||
предметный пучок 2-2 (предметная волна). Оба пучка должны быть когерентны. Опорный и предметный пучки, налагаясь друг на друга, образуют интерференционную картину, которая фиксируется фотопластинкой. После проявления фотопластинки и получается голограмма - зарегистрированная на фотопластинке интерференционная картина, образованная при сложении опорной и предметной волн.
Для восстановления изображения голограмму помещают в то самое место, в котором она находилась при фотографировании, и освещают опорным пучком света (рис. 33.10). Часть лазерного пучка, которая освещала предмет при фотографировании теперь перекрывается перегородкой.

В результате дифракции опорной волны на интерференционной структуре

Наиболее важное применение голографии – запись и хранение информации, а в будущем возможны голографическое кино и телевидение.
Вопросы для самоконтроля.
1. Какое явление называется дифракцией?
2. Сформулируйте принцип Гюйгенса-Френеля.
3. Что такое зона Френеля?
4. Как объяснить образование максимумов и минимумов с помощью принципа Гюйгенса-Френеля?
5. Как отличается дифракция Фраунгофера от дифракции Френеля?
6. Как объясняется появление «пятна Пуассона»?
7. Выведите формулу распределения интенсивности при дифракции Фраунгофера на одномерной щели.
8. Что представляет собой дифракционная решетка? Каково распределение интенсивности на экране за дифракционной решеткой? Как оно объясняется?
9. Каков принцип голографии? Каковы возможные применения голографии?
Лекция № 34
Дата добавления: 2015-06-12; просмотров: 2758;

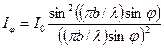
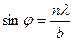
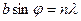
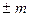 λ
λ