Физическая природа света
Большинство свойств света, таких как интерференция, дифракция, преломление и поляризация, могут быть объяснены на основе волновых представлений. Однако существуют явления (в частности фотоэффект, вынужденное и, особенно, спонтанное излучение), для объяснения которых необходимо привлекать квантовые представления.
Согласно квантовым представлениям свет представляет собой поток частиц малой энергии, которые называются фотонами. Фотоны являются элементарными квантами энергии светового излучения определенной частоты (длины волны) и не могут быть разделены на составные части без изменения частоты.
Энергия фотона определяется выражением:
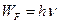(1.1)
где 
[Дж·с] – постоянная Планка,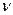 
– частота света [Гц]. Поскольку энергия фотонов растет с увеличением частоты, то важность учета квантовой природы света растет в области коротких длин волн.
Полезна взаимосвязь между единицами измерения частоты и энергии, используемыми в оптическом диапазоне (см. Таблицу 1).
Таблица 1. Единицы измерения энергии и частоты в оптике
| Единица измерений | Дж | эрг | °К | эВ | Гц | см-1 |
| Дж | 107 | 7,24·1022 | 6,24·1018 | 1,51·1033 | 5·1022 | |
| эрг | 10-7 | 7,24·1015 | 6,24·1011 | 1,51·1026 | 5·1015 | |
| °К | 1,38·10-23 | 1,38·10-16 | 8,62·10-5 | 2,08·1010 | 0,7 | |
| эВ | 1,6·10-19 | 1,6·10-12 | 1,16·104 | 2,42·1014 | 8,1·103 | |
| Гц | 6,626·10-34 | 6,626·10-27 | 4,8·10-11 | 4,15·10-15 | 3,3·10-11 | |
| см-1 | 2·10-23 | 2·10-16 | 1,44 | 1,24·10-4 | 3·1010 |
В соответствии с классическими представлениями свет – это распространяющаяся в пространстве электромагнитная волна, подчиняющаяся уравнениям Максвелла. Физически электромагнитная волна состоит из двух взаимно связанных векторных волн: электрической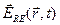 
и магнитной 
.
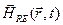Из уравнений Максвелла для свободного пространства легко получить дифференциальное уравнение в частных производных для электрического поля световой волны 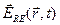, которое получило название волнового уравнения:
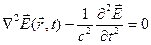(1.2)
где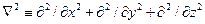 
- оператор Лапласа, 
- скорость света в вакууме,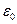 
и 
- электрическая и магнитная постоянные вакуума соответственно (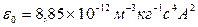 
, 
).
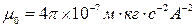Простейшим и важнейшим решением уравнения (1.2) является плоская линейно поляризованная монохроматическая электромагнитная волна. Направим ось z вдоль направления распространения плоской монохроматической световой волны, а направление x - вдоль направления электрического поля. Тогда выражение для амплитуды электрического поля имеет следующий вид.
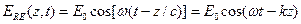
Плоская волна – в вакууме решением волнового уравнения является функция вида:
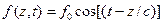
В случае плоских монохроматических электромагнитных волн тройка векторов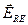 
, 
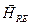и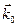 
взаимно ортогональна.
В плоской монохроматической световой волне интенсивность связана с амплитудой электрического поля следующим выражением:
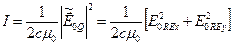. (1.2)
Поскольку действительная амплитуда электрического поля зависит не только от интенсивности световой волны, но и от поляризации, удобно ввести новое понятие – амплитуду световой волны
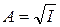. (1.3)
Комплексная амплитуда и вектор электрического поля плоской монохроматической волны связаны с амплитудой поля следующими выражениями:
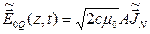. (1.4а)
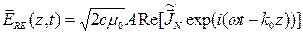. (1.4б)
Дата добавления: 2015-06-12; просмотров: 628;