Основные уравнения асинхронного двигателя.
Напряжение 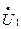 , приложенное к фазе обмотки статора, уравновешивается: э.д.с.
, приложенное к фазе обмотки статора, уравновешивается: э.д.с. 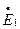 наведенной в обмотке статора основным (рабочим) магнитным потоком, э.д.с. рассеяния
наведенной в обмотке статора основным (рабочим) магнитным потоком, э.д.с. рассеяния 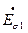 и падением напряжение на активном сопротивлении обмотки статора
и падением напряжение на активном сопротивлении обмотки статора 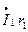 :
:
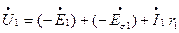 (3.27)
(3.27)
Или с учетом (3.24)
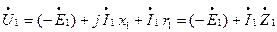 (3.28)
(3.28)
где 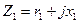 – сопротивление фазы обмотки статора.
– сопротивление фазы обмотки статора.
Уравнение (3.28) является уравнением напряжений обмотки статора.
При нагрузках двигателя, не превосходящих номинальную, 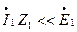 поэтому без большой погрешности можно считать, что:
поэтому без большой погрешности можно считать, что:
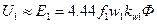 (3.29)
(3.29)
Так как действующее значение напряжения U1 при работе двигателя неизменно, то и магнитный поток Ф практически постоянен. Он, как и в трансформаторе, примерно равен потоку холостого хода Ф0 и также зависит от частоты f1 и числа витков w1.
Э.д.с. 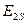 и
и 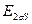 наводимые потоками Ф и
наводимые потоками Ф и 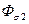 в обмотке ротора, уравновешиваются падением напряжения
в обмотке ротора, уравновешиваются падением напряжения 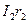 на активном сопротивлении обмотки ротора:
на активном сопротивлении обмотки ротора:
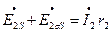 (3.30)
(3.30)
Учитывая (3.25) и преобразуя (3.30), получим
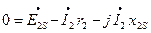 (3.31)
(3.31)
Это уравнение аналогично уравнению напряжений вторичной обмотки трансформатора в режиме короткого замыкания, когда U2 = 0. Однако в отличие от уравнения трансформатора, здесь имеются изменяющиеся с изменением частоты вращения двигателя (скольжения s) величины 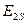 и
и 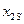 [см. (3.23) и (3.26)]. Наличие этих величин объясняется тем, что вторичная обмотка (обмотка ротора) вращается в пространстве.
[см. (3.23) и (3.26)]. Наличие этих величин объясняется тем, что вторичная обмотка (обмотка ротора) вращается в пространстве.
Перепишем уравнение (3.31) с учетом того, что 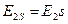 и
и 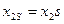 :
:
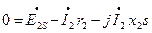 (3.32)
(3.32)
Поделив обе части уравнения на s, получим:
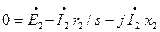 (3.33)
(3.33)
В уравнении (3.33) э.д.с. 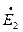 и сопротивление х2 не зависят от скольжения. Они представляют собой э. д. с. и индуктивное сопротивление рассеяния при неподвижном роторе (при s=1). Однако в уравнении появилось сопротивление
и сопротивление х2 не зависят от скольжения. Они представляют собой э. д. с. и индуктивное сопротивление рассеяния при неподвижном роторе (при s=1). Однако в уравнении появилось сопротивление 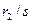 , зависящее от скольжения s. Таким образом, вращающийся ротор машины (с переменной
, зависящее от скольжения s. Таким образом, вращающийся ротор машины (с переменной 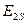 ) можно привести к неподвижному (с постоянной
) можно привести к неподвижному (с постоянной 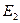 ), если вместо сопротивления
), если вместо сопротивления 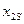 включить сопротивление
включить сопротивление 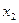 , а вместо сопротивления
, а вместо сопротивления 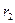 – сопротивление
– сопротивление 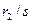 .
.
Вычтем из сопротивления 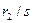 сопротивление
сопротивление 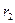 :
:
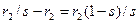 (3.34)
(3.34)
Сопротивление 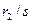 может быть записано в виде суммы двух сопротивлений:
может быть записано в виде суммы двух сопротивлений: 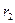 и
и 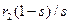 , т. е.
, т. е.
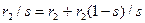 (3.35)
(3.35)
Преобразовав равенство (3.33) с учетом (3.35), запишем
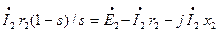 (3.36)
(3.36)
или
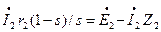 (3.37)
(3.37)
где 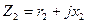 – сопротивление фазы обмотки ротора при n2 = 0 (s=1).
– сопротивление фазы обмотки ротора при n2 = 0 (s=1).
Уравнение (3.37) аналогично уравнению напряжений вторичной обмотки трансформатора с той лишь разницей, что вместо 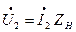 – выходного напряжения трансформатора, здесь в левой части стоит величина
– выходного напряжения трансформатора, здесь в левой части стоит величина 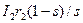 , по размерности одинаковая с выходным напряжением трансформатора U2. Это значит, что обмотка вращающегося ротора асинхронной машины подобна вторичной обмотке трансформатора, включенной на сопротивление
, по размерности одинаковая с выходным напряжением трансформатора U2. Это значит, что обмотка вращающегося ротора асинхронной машины подобна вторичной обмотке трансформатора, включенной на сопротивление 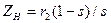 , зависящее от скольжения s (частоты вращения n2). Так же, как и в трансформаторе, величина
, зависящее от скольжения s (частоты вращения n2). Так же, как и в трансформаторе, величина 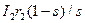 зависит от нагрузки, определяемой в асинхронном двигателе скольжением.
зависит от нагрузки, определяемой в асинхронном двигателе скольжением.
Уравнение м.д.с. асинхронной машины согласно (3.20) может быть записано в виде:
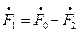 (3.38)
(3.38)
или, если выразить м.д.с. через токи 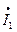 ,
, 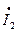 ,
, 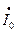 число полюсов р, числа витков w1 и w2, обмоточные коэффициенты kwl и kw2, а также и числа фаз m1 и m2:
число полюсов р, числа витков w1 и w2, обмоточные коэффициенты kwl и kw2, а также и числа фаз m1 и m2:
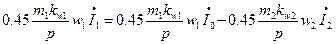
Разделив обе части равенства на 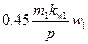 получим уравнение токов асинхронного двигателя:
получим уравнение токов асинхронного двигателя:
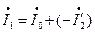 (3.39)
(3.39)
где 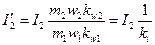 ток ротора, приведенный к числам витков и фаз обмотки статора.
ток ротора, приведенный к числам витков и фаз обмотки статора.
Коэффициент приведения тока ki, отличается от коэффициента трансформации трансформатора только наличием чисел фаз статора m1, ротора m2, и обмоточных коэффициентов kw1 и kw2.
Э.д.с. и сопротивления обмотки ротора, так же как э.д.с. и сопротивления вторичной обмотки трансформатора, обычно приводятся к числам витков и фаз первичной обмотки – обмотки статора:
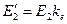 ,
, 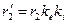 ,
, 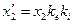 (3.40)
(3.40)
здесь 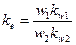 – коэффициент приведения э.д.с.
– коэффициент приведения э.д.с.
Уравнение напряжений обмотки ротора (3.36) в приведенных величинах имеет вид:
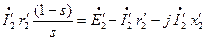 (3.41)
(3.41)
Уравнения напряжений обмотки статора (8.16), напряжений (э.д. с.) обмотки ротора (3.41) и токов (3.39) считаются основными уравнениями асинхронной машины.
Из рассмотрения этих уравнений следует, что они практически аналогичны основным уравнениям трансформатора, нагруженного сопротивлением 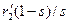 .
.
Это значит, что электромагнитные процессы, протекающие в асинхронной машине и трансформаторе, нагруженном сопротивлением 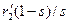 , аналогичны.
, аналогичны.
Дата добавления: 2015-06-12; просмотров: 869;
