Основные сведения. Под дифракцией обычно понимается явление «огибания» ЭМВ препятствия на пути распространения
Под дифракцией обычно понимается явление «огибания» ЭМВ препятствия на пути распространения. В настоящее время под дифракцией в широком смысле понимается поведение ЭМВ в некоторой области пространства, включающую границу раздела сред. К задачам дифракции относятся задачи о распространении ЭМВ в неоднородных средах, проникновение ЭМВ через отверстия в экранах или решетки, «огибания» ЭМВ различного рода препятствий [9, 10].
Формы и ЭМ параметры препятствий в разных задачах существенно отличаются. Решения задач являются сложными [5–13], в данном пособии рассмотрим только простейшие задачи дифракции.
При распространении ЭМВ в свободном пространстве области пространства по-разному влияют на формирование ЭМП на входе приемника.
Областью пространства, существенной при распространении ЭМВ, называют область, в которой распространяется основная часть передаваемой мощности.
Эта область охватывает пространство вблизи прямой, соединяющей точки расположения излучателя и приёмной антенны. Конфигурацию существенной области определяют исходя из принципа Гюйгенса – Френеля. Пусть в точке А помещен источник ЭМВ, а в точке В – приемная антенна (расстояние АВ много больше l). На некотором расстоянии от точки А помещена бесконечная плоскость, перпендикулярная к линии АВ (рис. 14.1). Эту плоскость рассматривают в качестве поверхности вторичных источников ЭМП и разбивают на зоны Френеля. Полное ЭМП в точке приема определяется суммированием элементарных вторичных ЭМП на плоскости S. Границы зон Френеля определяются как
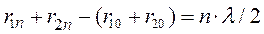. (14.1)
где n – натуральное число.
В плоскости S (рис. 14.1) уравнением (14.1) описываются концентрические окружности c радиусами Rn
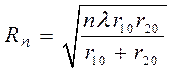. (14.2)
Площади всех зон одинаковы и равны
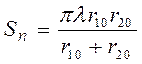. (14.3)
При перемещении плоскости Sвдоль прямой АВ для границ любой зоны Френеля будут справедливы равенства :
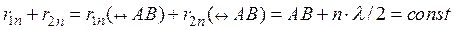. (14.4)
Каждой зоне Френеля в этом случае, как известно из аналитической геометрии, будет соответствовать эллипсоид вращения. Первая зона Френеля представляет собой эллипсоид вращения с фокусами в точках А и В. Зоны высших номеров – часть пространства между соседними эллипсоидами вращения [5, 34].
Таким образом, при конечном числе учитываемых зон Френеля конфигурация существенной области представляет собой эллипсоид вращения с фокусами в точках расположения излучателя и приёмника.
Согласно (14.1) вторичные источники, расположенные на границах двух соседних зон, излучают волны, приходящие в точку наблюдения в противофазе. Найдем суммарное поле, обусловленное всеми зонами Френеля. Разделив каждую зону Френеля на некоторое число равных по площади колец и сложив их амплитуды с учетом фазы, получим результирующую напряженность поля, создаваемого всеми зонами Френеля:
ES = Е1 – Е2 + Е3 – Е4 + ... (–1)nЕn+... (14.5)
Если антенны находятся в дальней зоне относительно плоскости S, то при переходе от одной зоны к другой амплитуда колебаний каждого элемента площади Sn изменяется незначительно, и тем более еще меньше изменяется амплитуда при перемещениях в пределах одной зоны.
Поскольку соседние члены ряда мало отличаются друг от друга, каждый член ряда можно считать равным среднему арифметическому из двух соседних:
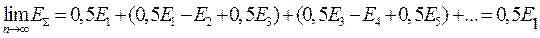. (14.6)
Двукратное уменьшение амплитуды результирующего ЭМП по сравнению с ЭМП первой зоны Френеля связано с тем, что ЭМВ от зон четных порядков приходят в точку приема в противофазе по отношению к ЭМВ от нечетных зон.
Результирующая напряженность поля в точке приема стремится к половине значения напряженности поля, создаваемого первой зоной.
Отсюда следует вывод: результирующее ЭМП в точке наблюдения создаётся в основном ЭМВ вторичных излучателей, расположенных в пределах нескольких первых зон Френеля. Вклад остальных зон Френеля в силу быстрой сходимости ряда (14.6) пренебрежимо мал. Если в качестве существенной области взять восемь первых зон, то ошибка в определении ЭМП составит лишь 16 % .
Таким образом, существенная при распространении ЭМВ область пространства ограничена эллипсоидом вращения, соответствующим внешней границе пространственной зоны Френеля с небольшим номером. Эллипсоид существенной области тем больше вытянут, чем меньше длина ЭМВ. При l®0 эллипсоид превращается в линию, соединяющую источник и приемник.
Список рекомендуемой литературы:[2, с. 139–150; 6, с. 343–379; 8, с. 45–57; 9, с. 342–376; 10, с. 342–376; 11, с. 174–187; 13, с. 222–241; 34, с. 24–25, 62–65; 35, с. 35–37, 90–95].
Контрольные вопросы и задания
1. Дайте определение явлению дифракции.
2. Дайте характеристику основным методам решения задач дифракции.
3. Каковы пределы применимости метода геометрической оптики?
4. Какие особенности имеет метод физической оптики?
5. Объясните основные идеи метода Фурье на примере дифракции ЭМП на металлическом цилиндре.
6. Дайте определение зонам Френеля и спирали Корню.
7. Какие особенности имеет дифракция Фраунгофера?
Тема 15. Условия распространения ЭМВ
в направляющих системах
Направляемые ЭМВ. Понятие о линиях передачи и направляющих системах. Типы регулярных линий передачи. Поперечные и продольные составляющие векторов ЭМП. Классификация ЭМВ. Е, Н, Т и гибридные ЭМВ.
Решение уравнений Гельмгольца для направляемых волн. Связь поперечных составляющих векторов ЭМП с продольными. Постоянная распространения, критическая частота (критическая длина волны), длина волны в линии передачи, фазовая скорость, характеристическое сопротивление, затухание.
Общие свойства волн типа Т, Е и Н. Скорость распространения энергии. Дисперсия. Понятие об одномодовом и многомодовом режимах работы. Мощность, переносимая ЭМВ в линии передачи.
Дата добавления: 2015-06-12; просмотров: 716;