Элементарные излучатели
Электрический диполь. Вид выражений (12.1) и (12.3) указывает на то, что ЭМП антенны можно представить как сумму полей ее отдельных частей с учетом взаимодействия распределений токов на каждой из них. Эти излучатели выбирают так, чтобы их ЭМП можно было сравнительно просто рассчитать, а также реально использовать как простейшие антенны. Упрощение в расчетах достигается тем, что некоторые размеры излучателей выбираются много меньше длины волны[36].
Простейшим из таких излучателей является антенна в виде маленького отрезка (l<<l), вырезанного из тонкого провода (излучатель длиной l симметрично расположен на оси z, рис. 12.2). В этом случае выражение (12.1) можно представить так:
. (12.8)
В силу сделанных ограничений функция е–ikR/R заменяется ее значением в точке (x0 = y0 = z0 = 0), и (12.8) записывается так:
. (12.9)
Представляющий поток вектора плотности тока через поперечное сечение провода внутренний интеграл для этого случая приближенно равен потоку z-й составляющей плотности тока (I(z0) – комплексная амплитуда тока через поперечное сечение):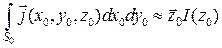 
.
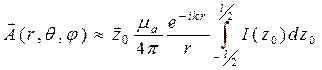. (12.10)
Поскольку kl=2πl/λ<<1, изменением тока вдоль провода пренебрегаем, тогда функцию I(z0) можно заменить постоянной I. В результате
. (12.11)
В ССК выражение (12.11) запишутся в следующем виде [1]:
, 
, 
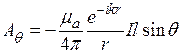. (12.12)
При выводе (12.11) нигде не использовано приближение дальней зоны. Поскольку размеры источника излучения много меньше длины волны, ЭМП любой сложной антенны можно представить как суперпозицию таких излучателей.
Учитывая, что I = iωq, уравнение (12.11) можно переписать так:
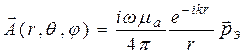, (12.13)
где 
– электрический дипольный момент системы из положительного и отрицательного зарядов, расположенных соответственно в точках (0, 0, +l/2) и (0, 0, – l/2). По этой причине этот излучатель называется «элементарным электрическим диполем», но также встречается и название «диполь Герца» [1].
Вычислим компоненты ЭМП с помощью формул (12.12) и (11.4) [1]
, 
,
, 
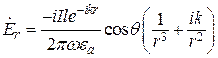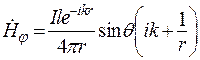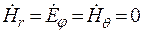. (12.14)
Для мгновенных значений из (12.14) с учетом (6.2) и (6.5) получим:
,
,
, 
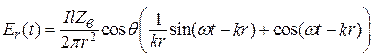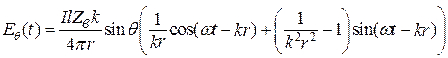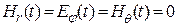. (12.15)
Из (12.14) и (12.15) следует, что векторы 
и 
взаимно перпендикулярны [1].
Найдем комплексный вектор Пойнтинга диполя Герца (4.6) [1]:
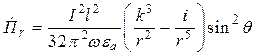
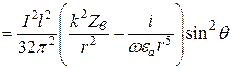; (12.16)
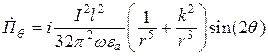. (12.17)
Величину Il называют моментом тока электрического диполя [1].
Для дальнейшего анализа целесообразно выделить ближнюю (kr << 1) и дальнюю зоны (kr >> 1) элементарного электрического диполя.
В данном случае условие дальней зоны, определяемое формулой (12.5), неверно. Это связано с «обрыванием» тока за пределами интервала (–kl/2, kl/2) [35].
Для ближней зоны уравнение (12.15) упрощается к виду
, 
,
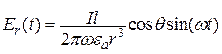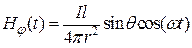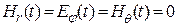, . (12.18)
В ближней зоне выполняется условие квазистационарности (r<<l/2π), и поэтому волновым характером ЭМП можно пренебречь. Векторные линии представляют собой концентрические окружности с центром на оси z.
Фазовый сдвиг между и составляет 90º, поэтому среднее за период значение 
равно нулю. Из формул (12.16)–(12.17) для ближней зоны получаем
, 
. (12.19)
Таким образом, в ближней зоне электрического диполя нет переноса энергии ЭМП, а преобладает колебательное (реактивное) поле.
Для дальней зоны из выражений (12.15) получаем
, ,
,
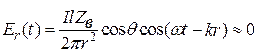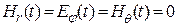. (12.20)
, 
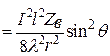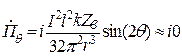. (12.21)
В дальней зоне Er можно пренебречь относительно поперечных компонент Eq и Hj . Компоненты Eq и Hj в дальней зоне синфазны, их соотношение равно 
, у вектора Пойнтинга преобладает радиальная составляющая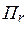 
.
Силовые линии лежат в меридиональной плоскости (проходит через ось z), а силовые линии 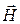– в азимутальной (экваториальной) (x0y или Q = 90º).
Нормированные ДН по полю (12.22) и ДН по мощности (12.23) симметричны относительно оси z, поэтому не зависят от φ (рис. 12.3):
, (12.22)
. (12.23)
Таким образом, излучение вдоль оси диполя Герца (ось z) отсутствует, ДН диполя представляет собой тор: проекцией ДН на азимутальную плоскость (плоскость 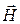) будет окружность, а на меридиональную (плоскость ) – «восьмерка», показанная на рис. 12.3 [1, 32].
Фазовая ДН не зависит от угловых координат, поверхность постоянной фазы представляет собой сферу с центром в начале координат. В этом случае говорят, что антенна имеет фазовый центр.
Поляризационная ДН определяется вектором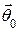 
, и соответственно ЭМП излучения имеет линейную поляризацию.
Для определения средней мощности излучения электрического диполя необходимо проинтегрировать 
по поверхности сферы, расположенной в дальней зоне. В случае вакуума получаем
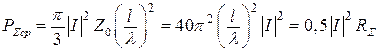. (12.24)
По аналогии с законом Джоуля – Ленца в формуле (12.24) выделяют величину RS , которую называют сопротивлением излучения
(для вакуума при l<<l ) . (12.25)
С увеличением l/l увеличивается эффективность излучения электрического диполя, но с увеличением l/l диполь перестанет быть элементарным (получается электрический вибратор [32], для анализа которого необходимо разбить вибратор на элементарные электрические диполи. ЭМП такой антенны представляет собой суперпозицию ЭМП элементарных электрических диполей.
Магнитный диполь.Хотя ЭМП любой антенны можно представить в виде суперпозиции полей элементарных электрических диполей, целесообразно также рассмотреть излучатели магнитного типа [1, 32].
С помощью принципа двойственности (11.16) произведем замену переменных в уравнениях (12.14)–(12.25).
Величина IМ l – момент тока магнитного диполя.
Магнитный диполь имеет такую же ДН (см. рис. 12.2), как электрический диполь. Однако у магнитного диполя силовые линии лежат в азимутальной плоскости, а силовые линии 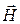– в меридиональной плоскости.
Если момент тока электрического диполя Il равен моменту тока магнитного диполя –IМl, то магнитное поле электрического диполя равно электрическому полю магнитного диполя, а электрическое поле электрического диполя отличается от магнитного поля магнитного диполя в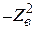 
раз [1, 32].
По аналогии с выражением (12.24) выделяют величину GМS , которую называют проводимостью излучения
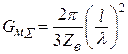(l<<l) , 
. (12.26)
При расположении магнитного диполя в вакууме
, 
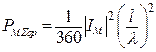. (12.27)
В реальных расчетах задача сводится к замене электрических диполей на магнитные. В других ситуациях (расчет щелевых антенн) роль магнитного тока играет удвоенное напряжение, приложенное между кромками щели.
Элементарные рамки с током.Простейшим примером магнитного излучателя является маленькая рамка с электрическим током (рис. 12.4), размеры которой много меньше длины волны. ЭМП такого излучателя не зависит от формы рамки. Магнитный момент рамки определяется формулой 
, где S – площадь рамки; направление нормали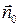 
выбирается по «правилу буравчика» относительно 
.
Для круговой рамки (S=πa2), симметричной относительно оси z, с равномерным распределением электрического тока векторный потенциал будет иметь лишь составляющую Aφ [1, 13].
После интегрирования по контуру круговой рамки (см. рис. 12.4) с учетом принятых упрощений в дальней зоне (ka >> 1) получим [1, 32]:
, 
,
, 
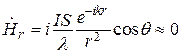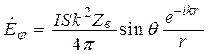. (12.28)
Излучение вдоль оси рамки (оси z) отсутствует, так как для каждого элемента 1 рамки с током (рис. 12.4) существует элемент 2 на противоположной стороне рамки, создающий ЭМП, которое компенсирует ЭМП элемента 1 (модули ЭМП, создаваемых элементами 1 и 2, одинаковы, а фазы противоположны) [1]. При отклонении точки наблюдения от оси рамки компенсирующий эффект уменьшается, и в плоскости рамки излучение будет максимально.
Сравнивая формулы (12.28) с формулами для магнитного диполя [1], заметим, что эти формулы совпадают при
или
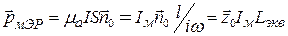. (12.29)
Из формулы (12.29) следует, что рассмотренная рамка с электрическим током эквивалентна магнитному диполю, расположенному на оси z, с моментом тока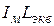 
, где 
[1, 32].
Для повышения эффективности электрической рамки как антенны ее выполняют из нескольких витков (n), в этом случае ISЭР=In, а значит:
(для вакуума) . (12.30)
Формулы для составляющих ЭМП элементарной рамки с магнитным током получим из соответствующих формул для рамки с электрическим током с помощью замены переменных в (11.16), согласно принципу двойственности.
Сравнивая формулы для составляющих ЭМП рамок (12.28), (12.29) с формулами для составляющих ЭМП диполей (12.20), получаем:
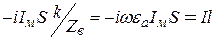или
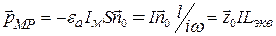. (12.31)
Из (12.31) следует, что рассмотренная рамка с магнитным током эквивалентна электрическому диполю, расположенному на оси z, с моментом тока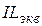 
, где [1, 32].
Проводимость излучения магнитной рамки
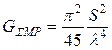(в случае вакуума) . (12.32)
Рассмотренные элементарные излучатели используются при анализе более сложных антенн, при этом их взаимосвязь можно выразить так:
« 
= 
« 
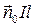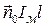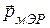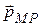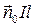= . (12.33)
Принцип эквивалентности. Принцип Гюйгенса. При определении ЭМП излучения вместо реальных источников удобно рассматривать их эквиваленты [1, 12, 36].
Выделим в пространстве V2 область V1, ограниченную замкнутой поверхностью S1 [1], которая охватывает все источники ЭМП.
ЭМП в пространстве V2, создаваемое сторонними источниками, расположенными в области V1, можно определить как поле излучения поверхностных источников на S1 [1, 10]. Эти соотношения выражают принцип эквивалентности, что и отражено в приводимых названиях:
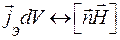– плотность поверхностных электрических токов;
– плотность поверхностных магнитных токов;
– плотность поверхностных электрических зарядов;
– плотность поверхностных магнитных зарядов. (12.34)
Из принципа эквивалентности следует, что ЭМП, создаваемые в точке наблюдения за счет полей, существующих на ограничивающей поверхности S1 , можно, как и для источников ЭМП в объеме, рассматривать как результат суперпозиции полей, создаваемых элементарными площадками поверхности S1 с соответствующим распределением исходных полей.
В соответствии с этим сформулирован принцип Х. Гюйгенса – Френеля, согласно которому каждый элемент произвольной замкнутой поверхности, окружающей источники ЭМП, можно рассматривать как вторичный источник, порождающий элементарную вторичную ЭМВ, а ЭМП в точке наблюдения представляет собой суперпозицию этих элементарных вторичных волн [1, 11].
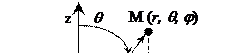Источник Гюйгенса.В теории антенн рассматривают еще один тип элементарного источника излучения, называемый источником Гюйгенса. Такой источник представляет собой элементарную плоскую площадку (рис. 12.5) с распределением поля в виде плоской ЭМВ линейной поляризации, волновой вектор которой направлен по нормали к площадке.
В соответствии с принципом эквивалентности (12.34), ЭМП такого излучателя представляет собой суперпозицию полей двух взаимно перпендикулярных элементарных диполей (электрического и магнитного), расположенных в начале координат в плоскости площадки (x0y). Рассмотрим соответствующую элементарную площадку площадью DS, расположенную в начале координат перпендикулярно оси z (рис. 12.5).
Пусть компонента Es параллельна положительному направлению оси x, а компонента Hs –положительному направлению оси y. Комплексные амплитуды данных компонент связаны через волновое сопротивление фронта волны. В соответствии с принципом эквивалентности касательные составляющие напряженностей ЭМП можно заменить поверхностными токами
; 
. (12.35)
Из (12.1) получаем с учетом дальней зоны и малости площадки
, 
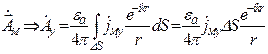. (12.36)
После перехода к ССК, получаем [1]
, 
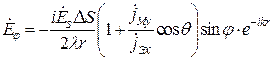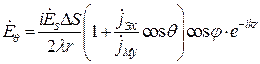, (12.37)
, 
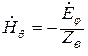. (12.38)
При условии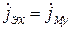 
формула (12.37) запишется в виде
,
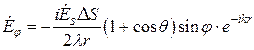. (12.39)
Нормированная ДН источника Гюйгенса (и соответственно системы из двух взаимно перпендикулярных электрического и магнитного диполей) представляет собой поверхность вращения кардиоиды (1+cosq)/2(рис. 12.6) вокруг оси, перпендикулярной площадке (оси z).
В отличие от отдельно взятых электрического и магнитного диполей такой источник ЭМП имеет четко выраженную направленность: максимум в направлении движения фронта волны (q = 0) и минимум в противоположном направлении (q = p) (см. рис. 12.6 и 12.5) [1, 32].
При анализе апертурных антенн (зеркальные и т. п.) итоговое ЭМП получается как суперпозиция ЭМВ, создаваемых излучателями Гюйгенса, с заданными электрическими и магнитными полями на них.
Излучающие и неизлучающие системы. Представим себе отрезок разомкнутой на одном конце двухпроводной линии длины l, подключенной на другом конце к генератору синусоидальных колебаний частоты w (рис. 12.7а). Поперечные размеры линии выбраны так (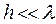 
), что в линии существует лишь Т-волна. Следовательно, токи в проводах линии противофазны, и в дальней зоне линия практически не излучает.
  |
Распределение тока вдоль линии соответствует стоячей волне с узлом на разомкнутом конце. Его можно записать в таком виде [1, 36]
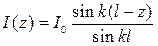, (12.40)
где 
– комплексная амплитуда тока в пучности; 
.
По мере развертывания проводов (рис. 12.7б) будут также возбуждаться волны других типов с замкнутыми силовыми линиями, способные распространяться и в области вне проводов. В итоге получается электрический вибратор (рис. 12.7в) – эффективная излучающая система. Так наглядно можно описать превращение практически неизлучающей системы в излучающую [1].
Самое замечательное при этом заключается в том, что при выполнении условий: d << l, d << l – распределение тока в проводах почти сохраняется, но с учетом симметрии расположения проводов вибратора и выражения (12.40) принимает вид
. (12.41)
Аналогичным образом можно описать превращение плоского конденсатора в вибраторную антенну (рис. 12.8).
Список рекомендуемой литературы:[1, гл. 15, 16, с. 88–90, 92–106; 2, с. 126–139; 5, с. 52–58; 6, с. 318–342; 8, с. 29–37, 62–76; 9, с. 78–133, 155–160; 10, с. 78–131, 143–159; 11, с. 106–129; 12, с. 152–155, 163–181; 13, с. 56–64, 150–174; 32, с. 13–34; 34,с. 12–21; 35,с. 6–32; 36,с. 7–30].
Контрольные вопросы и задания
1. Какие системы координат удобны для анализа излучающих систем?
2. Покажите целесообразность введения электродинамических потенциалов для решения задач излучения.
3. На какие зоны можно разделить пространство около антенны?
4. Каковы общие свойства поля излучения системы токов?
5. На каких расстояниях от антенны располагается дальняя зона?
6. Каковы особенности ЭМП в дальней зоне?
7. Какая характеристика антенны является основной?
8. Дайте определение векторов Герца.
9. Дайте определение основным разновидностям элементарных излучателей.
10. Как можно создать эквивалент магнитного диполя?
11. Назовите основные параметры излучателей.
12. Опишите особенности излучения элементарных излучателей.
13. Дайте определение и опишите параметры элемента Гюйгенса.
14. Дайте определение сопротивлению и проводимости излучения.
Дата добавления: 2015-06-12; просмотров: 3484;