Колебания струны

В натянутой струне, закрепленной с обоих концов, при возбуждении произвольного поперечного возмущения может возникать стоячая волна. При этом на закрепленных концах струны должны выполняться определенные граничные условия: концы струны должны быть узлами стоячей волны. Это означает, что на длине струны 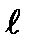укладываться целое число 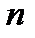полуволн: 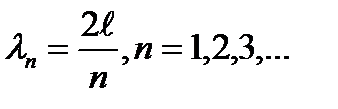Соответствующие этим длинам волн частоты где фазовая скорость распространения бегущей волны в струне - сила натяжения струны, 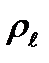- линейная плотность, т.е. масса единицы длины струны. Частоты 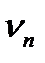называются собственными частотами струны. а соответствующие им гармонические колебания – собственными колебаниями, или гармониками. Частота 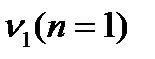называется основной частотой, а остальные частоты (n = 2,3,…) – обертонами (рис.2).В общем случае колебания струны представляют собой суперпозицию (наложение) различных гармоник.

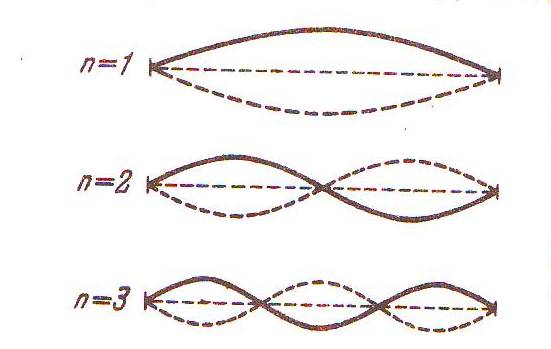
Рис.2

Колебания струны примечательны в том отношении, что для них по классическим представлениям получаются дискретные значения одной из характеристик колебательного движения величин – частоты. Для классической физики такая дискретность – исключение, в то время как для квантовых процессов дискретность является скорее правилом, чем исключением.