Порядок выполнения эксперимента
1.При включенном стенде и отсутствии входного напряжения произвести балансировку усилителя потенциометром “установка 0”.
2. Для инвертирующего (рис.5.4) или неинвертирующего (рис.5.5) усилителя снять передаточные характеристики для заданных в предварительном задании значений Rо.с. Входное напряжение снимается с источников опорного напряжения с полярностью “+” и “-”, устанавливаемой переключателями П1 и П2 . Уровень входного напряжения меняется в диапазоне от 0 до 1000 мВ. Результаты измерений занести в табл.5.1.
Таблица 5.1
| Uвх, мВ | … | ||
| U¢вых, В при Rо.с.=20 кОм | … | ||
| U²вых, В при Rо.с.=100 кОм | … | ||
| U²¢вых, В при Rо.с.=270 кОм | … |
По результатам измерений построить передаточные характеристики. Недостающие характеристики в трех четвертях системы координат строятся по зеркальному отображению по отношению к снятым по табл.5.1. На построенных характеристиках нанести точки по предварительному расчету.
3. Собрать цепь вычитателя-усилителя согласно рис.5.6 и подать на входы от источников постоянного тока напряжения различные по уровню и знаку при различных значениях Rо.с. Значения входных и выходного напряжений занести в табл.5.2.
4. а) Для инвертирующего (рис.5.7) или неинвертирующего (рис.5.8) цифрового сумматора произвести измерения входных и выходного напряжений для различных по знаку и величине входных напряжений при двух значениях Rо.с. По п.п. 3,4 уровень входных напряжений брать в пределах ± 1В. Результаты измерений занести в табл.5.2.
Таблица 5.2
| Uвх1, мВ | Uвх2, мВ | Uвых, мВ | Rо.с, кОм | Uвых, расч., мВ | |
| Вычитатель | |||||
| Сумматор | |||||
б) В геометрическом неинвертирующем сумматоре на входы подаются переменные напряжения: первое - с выхода симметричного мультивибратора стенда (включить источник питания 5В стенда), второе - с генератора низкочастотных сигналов (синусоидальный выход). Ослабление - 20. Частота 3-6 кГц. Rо.с сумматора 10 или 20 кОм. Снять осциллограммы входных uвх(t) и выходного uвых(t) напряжений, по которым определить параметры входных сигналов (амплитуду, частоту, период). Произвести графическое сложение входных сигналов с коэффициентом усиления ku=2.
5. По рис.5.9 и 5.10 на входы дифференциатора и интегратора подаются прямоугольные импульсы с выхода симметричного мультивибратора стенда. Снять осциллограммы и определить параметры входных uвх(t) импульсов (амплитуда, период, частота), а также снять осциллограммы выходных uвых(t) напряжений при следующих номинальных данных устройств: для дифференциатора - Cвх=10 и 5 нФ, Rо.с=20 и 30 кОм, Cо.с=2 нФ; для интегратора - Rвх=10 кОм, Cо.с=10 и 5нФ, Rо.с=20 кОм. По снятым осциллограммам определить графическим способом постоянную времени t и сравнить с результатами предварительного расчета.
6. Собрать схему линейного усилителя согласно рис.5.12 с подключением на вход генератора низкочастотных колебаний (синусоидальный выход). Снять амплитудную характеристику на частоте 1кГц в линейном режиме, который контролируется осциллографом на выходе усилителя, для значений Rо.с=91 и 270 кОм. Результаты эксперимента свести в табл.5.3.
Таблица 5.3
| Rо.с=91кОм | Uвх, мВ | |||
| Uвых, В | ||||
| Rо.с=270кОм | Uвх, мВ | |||
| Uвых, В |
По результатам измерений построить соответствующую характеристику Uвых=f(Uвх).
7. По рис.5.13 собрать схему избирательного усилителя. На вход подключается низкочастотный генератор сигналов на синусоидальном выходе с уровнем выходного напряжения 90 мВ (входное для усилителя). Снять амплитудно-частотную характеристику ku(f) в диапазоне частот 4,5-7,5 кГц. Результаты эксперимента занести в табл.5.4.
Таблица 5.4
Uвх=90мВ
| f, кГц | |||
| Uвых, В | |||
| ku |
По результатам табл.5.4 построить АЧХ, определить резонансную частоту, которую сравнить с результатами предварительного расчета. По АЧХ определить fн, fв, полосу пропускания.
8. Согласно рис.5.14 и 5.15 при включенном питании стенда снять осциллограммы выходных uвых(t) напряжений мультивибратора и генератора гармонических колебаний, по которым определить параметры сигналов: амплитуду, частоту, период. Результаты эксперимента сравнить с результатами предварительного расчета.
9. На вход генератора линейно-изменяющегося напряжения (ГЛИН) по схеме рис.5.15 подать uвх от несимметричного мультивибратора. По осциллограммам uвх(t) и uвых(t) определить: для uвх - частоту, коэффициент заполнения, скважность импульсов, для uвых - амплитуду, длительность прямого (рабочего) хода, длительность обратного хода.
10. На вход компаратора (рис.5.17) подать синусоидальное напряжение от генератора сигналов при ослаблении “0”. Снять осциллограммы входного uвх(t) и выходного uвых(t) напряжений.
11. Для триггера Шмитта (рис.5.18) при подаче на вход напряжения (по п.10) снять передаточную характеристику uвых(uвх) устройства.
Примечание: п.п.4б, 5, 9, 10, 11 выполнять, используя оба канала осциллографа (канал А - вход, канал Б - выход). Внимание! Перед включением осциллографа в схему обязательно проверьте положение входа “^“ (общая точка схемы).
Содержание отчета
Цель работы, рабочие схемы исследуемых устройств, результаты предварительного расчета, характеристики, осциллограммы, рассчитанные параметры.
Контрольные вопросы
1. К какому классу усилителей относится ОУ? 2. Чем объясняется широкое использование ОУ? 3. Поясните структурную компоновку ОУ. 4. Что такое обратные связи в усилителях и как они используются при построении конкретных устройств на базе ОУ? 5. Какие основные характеристики ОУ и какой они имеют вид? 6. Где используют линейный и нелинейный режим усиления? 7. Поясните принцип построения инвертирующего и неинвертирующего усилителя на базе ОУ. 8. Как определяется их коэффициент усиления? 9. Поясните принцип построения вычитателя, сумматора, дифференциатора, интегратора. Запишите формулы выполняемых операций. 10. Что такое “избирательный усилитель”? Особенности АЧХ. Что такое и как определяется полоса пропускания? 11. Основные принципы построения самовозбуждающихся устройств на базе ОУ. 12. Что такое частотно-зависимые цепи и в каких устройствах они используются? 13. Принцип построения и использование ГЛИНа. 14. Что такое “пороговые устройства”? 15. Какое принципиальное отличие при построении компаратора и триггера Шмитта на ОУ? 16. Поясните, что такое “гистерезис” в электронных цепях?
Лабораторная работа № 6
ЛОГИЧЕСКИЕ ФУНКЦИИ И МИКРОСХЕМЫ
Цель работы: изучение принципов построения серийных логических микросхем; исследование логических функций одного и двух переменных и их реализация; построение простых устройств автоматики на базе логических и цифро-импульсных устройств.
Общие сведения
Логические элементы (ЛЭ) широко применяются в автоматике, вычислительной технике и цифровых измерительных приборах. Их создают на базе электронных устройств, работающих в ключевом режиме, при котором уровни сигналов могут принимать только два значения. В положительной логике принято, что высокий уровень сигнала соответствует логической единице (1), а низкий – логическому нулю (0).
Все логические устройства можно разделить на две группы :
1) комбинационные, в которых выходные сигналы в данный момент однозначно определяются входными сигналами;
2) последовательностные, в которых выходные сигналы зависят не только от входных сигналов, но и от предыдущего состояния устройства.
Логическая функция выражает зависимость выходных логических переменных от входных и принимает значения 0 или 1. Любую логическую функцию удобно представить в виде таблицы состояний (таблицы истинности), где записываются возможные комбинации аргументов и соответствующие им функции.
| Таблица 6.1 | |||
| Название | Обозначение | Значение x | |
| функции | функции | ||
| Нулевая | y0 | ||
| Повторение | y1 | ||
| Инверсия | y2 | ||
| Единичная | y3 |
В общем случае число элементарных логических функций от n переменных равно 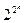 . Так, при одной переменной возможны четыре функции (табл.6.1). Здесь единичная и нулевая функции не зависят от значения аргумента и являются постоянными. Двум переменным соответствует 16 функций:
. Так, при одной переменной возможны четыре функции (табл.6.1). Здесь единичная и нулевая функции не зависят от значения аргумента и являются постоянными. Двум переменным соответствует 16 функций: 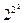 =16. В табл. 6.2 приведены основные логические функции двух переменных.
=16. В табл. 6.2 приведены основные логические функции двух переменных.
Работу логических устройств анализируют с помощью алгебры логики (булевой алгебры), где переменная может принимать только два значения: 0 или 1.
Основными логическими операциями являются (см. табл.6.2):
1) логическое умножение: y=x1·x2·...·xn (читается “и х1, и х2,..., и хn”);
2) логическое сложение: y=x1+x2+...+xn (читается “или х1, или х2,..., или хn”);
3) логическое отрицание: 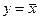 (читается “не х”).
(читается “не х”).
Как видно из табл. 6.2, выходной сигнал y элемента ИЛИ равен 1, если хотя бы один из его входов подан сигнал 1. Элемент И выдает 1, если на все входы поданы сигналы 1.
Все возможные логические функции n переменных можно образовать с помощью комбинации трех основных операций: И, ИЛИ, НЕ. Поэтому такой набор называют логическим базисом или функционально полным. Используя законы булевой алгебры (табл. 6.3), можно доказать, что таковыми являются наборы из одной функции И-НЕ, ИЛИ-НЕ.
В базовых элементах одной серии использована одинаковая микросхемная реализация. Серия характеризуется общими электрическими, конструктивными и технологическими параметрами.
 Интегральные микросхемы серии 155 представляют собой транзисторно-транзисторные логические (ТТЛ) элементы с 14 или 16 выводами. Базовым элементом серии является логический элемент И-НЕ, состоящий из многоэмиттерного транзистора VT1 и сложного усилителя-инвертора (рис.6.1).
Интегральные микросхемы серии 155 представляют собой транзисторно-транзисторные логические (ТТЛ) элементы с 14 или 16 выводами. Базовым элементом серии является логический элемент И-НЕ, состоящий из многоэмиттерного транзистора VT1 и сложного усилителя-инвертора (рис.6.1).
Если на входы ЛЭ поданы высокие положительные потенциалы 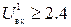 В, то переходы база-эмиттер VT1 закрываются, а через его открытый переход база-коллектор и резистор R1 протекает ток базы транзистора VT2, достаточный для его насыщения. При этом ток эмиттера VT2 открывает транзистор VT3 и подключает выход ЛЭ к общей шине. Вследствие падения напряжения на резисторе R2, а также за счет включения диода VD напряжение на переходе база-эмиттер транзистора VT4 оказывается недостаточным для его открывания.
В, то переходы база-эмиттер VT1 закрываются, а через его открытый переход база-коллектор и резистор R1 протекает ток базы транзистора VT2, достаточный для его насыщения. При этом ток эмиттера VT2 открывает транзистор VT3 и подключает выход ЛЭ к общей шине. Вследствие падения напряжения на резисторе R2, а также за счет включения диода VD напряжение на переходе база-эмиттер транзистора VT4 оказывается недостаточным для его открывания.
Таблица 6.2
| Тип элемента | Логическая функция (операция) | Обозначение логической операции | Таблица истинности | Условное изображение | ||||
| x1 | ||||||||
| x2 | ||||||||
 Элемент НЕ
(инвертор) Элемент НЕ
(инвертор)
| Логическое отрицание, инверсия | 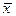 ùx
ùx
| x | x 1 y
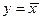
| ||||
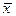
| ||||||||
 Элемент И
(конъюнктор) Элемент И
(конъюнктор)
| Логическое умножение, конъюнкция | x1·x2 x1x2 x1Ùx2 x1&x2 | x1·x2 | x1 & y x2 y=x1×x2 | ||||
 Элемент ИЛИ
(дизъюнктор) Элемент ИЛИ
(дизъюнктор)
| Логическое сложение, дизъюнкция | x1+x2 x1Úx2 | x1+x2 | x1 1 y x2 y=x1+x2 | ||||
 Элемент И-НЕ
(элемент
Шеффера) Элемент И-НЕ
(элемент
Шеффера)
| Штрих Шеффера, отрицание конъюнкции | _____ x1·x2 x1½x2 | _____ x1·x2 |
x1 & y
x2
y= 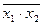
| ||||
 Элемент
ИЛИ-НЕ
(элемент
Пирса) Элемент
ИЛИ-НЕ
(элемент
Пирса)
| Стрелка Пирса, функция Вебба, отрицание дизъюнкции | _____ x1+x2 x1¯x2 | _____ x1+x2 |
x1 1 y
x2
y= 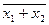
| ||||
 Запрет x2 Запрет x2
| Запрет | __ x1·x2 | __ x1·x2 |
x1 & y
x2
y=x1· 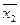
| ||||
 Импликация от x2 к x1 Импликация от x2 к x1
| Импликация | __ x1+x2 | __ x1+x2 |
x1 1 y
x2
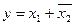
| ||||
 Исключающее ИЛИ (неравнозначность, сложение по модулю 2) Исключающее ИЛИ (неравнозначность, сложение по модулю 2)
| Исключающее ИЛИ | x1Åx2
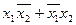
| x1Åx2 | x1 =1 y x2 y=x1Åx2 | ||||
 Равнозначность (эквивалентность) Равнозначность (эквивалентность)
| Равнозначность | x1~x2
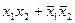
| x1~x2 | x1 = y x2 y=x1~x2 |
Таблица 6.3
| Аксиомы (тождества) | 1+х=1
0+х=х
х+х=х
х+ 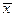 =1 =1
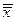 =х =х
| 0·х=0
1·х=х
х·х=х
х· 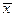 =0 =0
|
| Законы коммутативности | х1+х2=х2+х1 | х1·х2= х2·х1 |
| Законы ассоциативности | х1+х2+х3=х1+(х2+х3) х1·х2·х3=х1·(х2·х3) | |
| Законы дистрибутивности | x1·(х2+х3)=(х1·х2)+(х1·х3) x1+(х2·х3)=(х1+х2)·(х1+х3) | |
| Законы дуальности (теоремы де Моргана) | 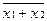 = = 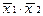
| 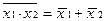
|
| Законы поглощения | х1+х1·х2= х1 | х1·(х1+х2)=х1 |
Таким образом, напряжение на выходе ЛЭ не превышает напряжения насыщения транзистора VT3 (примерно 0,2 …0,4 В), что соответствует логическому 0.
Если хотя бы на одном из входов ЛЭ оказывается низкий потенциал, 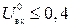 В, то через открытый переход база-эмиттер VT1 и резистор R1 протекает входной ток
В, то через открытый переход база-эмиттер VT1 и резистор R1 протекает входной ток 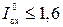 мА, а в базу VT2 попадает незначительный по величине обратный ток коллекторного перехода VT1. В этом случае транзисторы VT2 и VT3 заперты, а транзистор VT4 открыт и насыщен, так как в его базу протекает ток через резистор R2. Выход ЛЭ от шины питания +5 В получает высокий потенциал (логический уровень 1) через переходы VT4, диод VD и резистор R4.
мА, а в базу VT2 попадает незначительный по величине обратный ток коллекторного перехода VT1. В этом случае транзисторы VT2 и VT3 заперты, а транзистор VT4 открыт и насыщен, так как в его базу протекает ток через резистор R2. Выход ЛЭ от шины питания +5 В получает высокий потенциал (логический уровень 1) через переходы VT4, диод VD и резистор R4.
Данный ЛЭ производит логическое умножение двух входных сигналов с одновременным инвертированием выходной величины (2И-НЕ).
Если в базовом элементе (рис.6.1) отсоединить элементы R4, VT4, VD, а в коллектор транзистора VT3 включить нагрузку, то вместо инвертирования обеспечивается повторение выходного сигнала.
В настоящее время применяется несколько разновидностей серий микросхем с элементами ТТЛ: стандартные (серии 133; К155), высокого быстродействия (серии 130; К131), микромощные (серия 134), с диодами Шоттки (серии 530; К531) и микромощные с диодами Шоттки (серия К555). Кроме расширения номенклатуры элементов серий К531 и К555 сейчас активно развиваются наиболее перспективные серии ТТЛШ - микромощная К1533 и быстродействующая К1531, выполненные на основе последних достижений технологии изготовления ИС - ионной имплантации и прецизионной фотолитографии.
Наибольшим быстродействием обладают ЛЭ, выполненные по технологии ЭСЛ (эмиттерно-связанная логика) и ТТЛШ (транзисторно-транзисторная логика с транзисторами Шоттки). Меньше потребляет мощности КМДПТЛ (комплементарная МДП-транзисторная логика). Она же лучшая по помехоустойчивости и нагрузочной способности. ЭСЛ и И2Л (интегральная инжекционная логика) меньше других генерируют помехи.
В последние годы получили развитие программируемые логические элементы, на которых с помощью программаторов можно построить многие цифровые устройства.
Любая сложная логическая функция может быть реализована с помощью ЛЭ, выполняющих элементарные функции И-НЕ, ИЛИ-НЕ. Пусть требуется составить комбинационную схему с четырьмя входами x1, x2, x3, x4 и одним выходом y. Высокий уровень напряжения должен появляться на выходе только при наличии высоких уровней на трех входах, т.е. y=1 при x1=x2=x3=1 и x4=0. Такую схему можно составить путем подбора элементов. Например, элемент 3И-НЕ при подаче на его входы x1=x2=x3=1 дает на выходе сигнал y1=0. Подавая его и x4=0 на вход элемента 2ИЛИ-НЕ, получаем y=1.
Другим способом является преобразование логической функции по правилам алгебры логики (см. табл. 6.3). Для данного примера 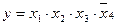 . Используя тождество
. Используя тождество 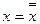 и формулы де Моргана, эту функцию можно представить в виде:
и формулы де Моргана, эту функцию можно представить в виде:
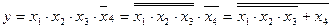 .
.
Полученной логической функции соответствует схема рис.6.2.

Предварительное задание к эксперименту
Составить на логических элементах 2И-НЕ (3И-НЕ) и 2ИЛИ-НЕ комбинационную схему, на выходе которой высокий уровень напряжения (логическая 1) появляется только при значениях сигналов на входах, заданных табл. 6.4.
Таблица 6.4
| Вариант | ||||||||
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | - | - | - | - |
Порядок выполнения эксперимента
Изучить принцип работы логических элементов (табл.6.2).
Подавая сигналы с наборного поля на входы логических элементов и соединяя их выходы с элементами индикации, реализовать основные функции одного и двух аргументов. Привести таблицы истинности исследуемых элементов.
Собрать схему предварительного задания, проверить правильность работы, составить таблицу истинности.
Осуществить выборку с наборного поля следующих чисел (по указанию преподавателя):
| а) всех четных | б) всех нечетных |
| в) всех чисел 8£N£15 | г) всех чисел N£7 |
| д) всех чисел, кратных 4 | е) чисел 0, 1, 2, 3 |
| ж) чисел 4, 5, 6, 7 | з) чисел 8, 9, 10, 11 |
| и) 3, 7, 11, 15 | к) 6, 7, 14, 15 |
| л) 4, 5, 12, 13 | м) 2, 6, 10, 14 |
| н) 2, 3, 10, 11 | о) 9, 11, 13, 15 |
| п) 8, 10, 12, 14 | р) 1, 5, 9, 13 |
| с) 1, 3, 9, 11 | т) 4, 6, 12, 14 |
| у) 10, 11, 14, 15 | ф) 1, 2, 5, 6, 9, 10, 13, 14 |
| х) 0, 3, 4, 7, 8, 11, 12, 15 | ц) 0-3, 8-11. |
5. Собрать схему, реализующую мажоритарную логику (на выходе появляется 1, если на всех трех или на любых двух входах имеется 1).
Содержание отчета
Цель работы; схема базового логического элемента; схема, составленная в предварительном задании; таблицы истинности исследуемых логических элементов; схемы по пп. 4, 5.
Контрольные вопросы
1. Какие операции и тождества алгебры логики Вы знаете? 2. Перечислите логические функции одного и двух аргументов, покажите примеры реализации. 3. Что представляет собой серия цифровых (логических) ИС? 4. Приведите примеры простейших цифровых устройств на основе логических элементов. 5. Реализуйте несколько функций, заданных таблицей истинности. 6. Какой набор логических элементов называют функционально полным (базовым)? 7. Поясните работу базового логического элемента. 8. Как классифицируются ЛЭ по микросхемной реализации. 9. Объясните причины перспективности интегральных логических элементов.
Лабораторная работа № 7
Дата добавления: 2015-06-10; просмотров: 978;
