Уявлення про еліпсоїд деформації та використання моделей такого еліпсоїда
для визначення кількісних характеристик пластичних деформацій гірських порід
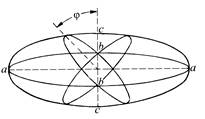 |
Поняття про еліпсоїд деформації було введено Г.Беккером у 1893 р. на основі уявлення про перетворення кулі при деформації на дво- або тривісний еліпсоїд. Відхилення розміру осей еліпсоїда від розміру осей первинної кулі відповідає величині деформації вздовж його головних осей (а, в, с). У напрямку максимального стиснення розташовується найменша вісь такого еліпсоїда – с, а в напрямку максимального розтягання – найбільша, а (рис. 1.2.11).
Рис. 1.2.11. Еліпсоїд напружень-деформації (пояснення в тексті)
Еліпсоїд напружень.При пружній деформації з основними осями еліпсоїда збігаються напрямки векторів головних нормальних напружень. Зокрема, вісь деформації а співпадає з головними напруженнями максимального розтягання, а вісь с – з максимальним напруженням стиснення. Вісь в займає проміжне положення. Що ж стосується найбільших дотичних напружень у такому еліпсоїді, то вони знаходяться у двох кругових перетинах, які утворюють кут (j) із віссю стиснення. При пружній деформації цей кут теоретично дорівнює 45°.
Подібний еліпсоїд називають еліпсоїдом нормальних напружень чи просто напружень.
Формально еліпсоїд напружень демонструє співвідношення напружень і деформації. Але його використання для визначення кількісних залежностей напружень від величини деформації чи, навпаки, в геологічних середовищах носить обмежений характер. Справа в тому, що він моделює ідеальні пружні деформації гомогенного (однорідного за всіма показниками) середовища, які керуються законом Гука. Реальні деформації тіл у природних умовах далеко не завжди відповідають пружним. Тому подібний еліпсоїд більш-менш коректно можна використовувати тільки для визначення кількісних характеристик деформацій тих середовищ (ділянок земної кори), властивості котрих наближаються до пружних.
У середовищах з низькою межею текучості еліпсоїд деформації використовують тільки як модель, котра демонструє кількісні характеристики зміни форми тіла при деформації розтягання–стиснення та простого зсуву. При цьому використовуються моделі еліпсоїдів видовження–скорочення (розтягання–стиснення) та обертання.
Модель еліпсоїда видовження–скорочення (розтягання–стиснення).Така модель класично була використана Е.Клоосом (1958) для аналізу складчастих дислокацій на прикладі деформованих оолітів. Цей дослідник до оолітів відносить породи, які складається з ооїдів – дрібних (розміром від 1,2 до 0,33 мм) тіл сферичної чи еліпсоїдальної форми, які виникли в результаті росту від центра до периферії. Ооїди володіють або радіальною структурою, або складаються з концентричних шарів.
Деформовані ооїди у відзначених породах мають форму тривісного еліпсоїда (рис. 1.2.12), який у системі структурних координат характеризується нерівністю: а>b>c. Вісь a при цьому характеризує максимальне видовження ооїдів, вісь c – навпаки, максимальне їх стиснення. При цьому перша вісь збігається з напрямком тектонічного транспортування (течії) матеріалу. Що ж стосується осі b, то вважається, що в складчастих структурах вона паралельна шарніру складки.
Є.Клоос вважав, що деформовані ооїди не є еліпсоїдами деформації, тому що вони не володіють однорідною будовою і деформуються пластично з перебільшенням межі пружності. З його позиції, ооїди демонструють лише ступені деформованості й напрямок течії.
| |
Визначення величини розтягання та стиснення виконується за наступними формулами:
1) максимальне розтягання – a×100%/r
2) максимальне стиснення – c×100%/r,
де r – радіус первинної фігури, а a,b, c – півосі еліпсоїда. При цьому радіус вираховується за формулою
r3=abc.
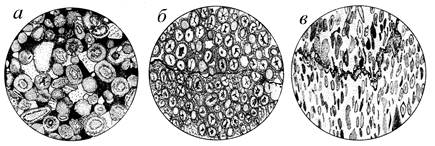
Рис. 1.2.12. Приклади деформації (б – слабкої і в – сильної) ооїдів порівняно з недеформованими їх аналогами (а) (за Е.Клоосом, 1958)
За якістю тензодатчиків, крім ооїдів, використовують будь-які інші геологічні тіла, первинна форма котрих більш-менш близька до круглої або ізометричної. До таких тіл, наприклад, належать мигдалини та "подушки" у вулканічних породах, більш-менш ізометричні ксеноліти, зерна і агрегати зерен, порфірові виділення та порфіробласти в кристалічних магматичних та метасоматичних породах, галька, рештки фауни та флори в осадових породах та багато інших подібних за формою мезо- та мікротіл.
В усіх відзначених випадках задача з визначення ступенів деформації коректно розв'язується лише в тому випадку, коли в'язкість відзначених включень не відрізняється або близька до в'язкості матриці, в якій вони знаходяться. В інших випадках деформація
Модель еліпсоїда обертання. Подібна модель, звичайно, використовується для вивчення кількісних характеристик простого зсуву. Є.І.Паталаха (1981) використав цю модель для визначення ступенів деформованості порід при кліважній течії, котра якнайближче відповідає моделі відзначеного зсуву (рис. І.2.13).
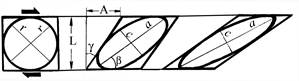
Рис. 1.2.13. Аналіз зсувної деформації на прикладі двовісної моделі еліпсоїда обертання (досліджується квадрат та вписане в нього коло). Пояснення в тексті
Якщо в тілі, що зазнає однорідної плоскої деформації, виділити квадрат та вписане в нього коло радіусом r з осями а і с, які відповідають осям розтягу та стиснення й на початку орієнтуютьсяпід кутами 45° до площини зсуву (максимальних дотичних напружень), зсув приведе до перетворення цього квадрата на трапецію (ромб), а коло – в еліпс з осями a>c. При зростанні деформації вісь а поступово видовжується, а вісь с, навпаки, скорочується. Крім того, обидві осі змінюють свою орієнтацію, обертаючись у напрямку зсуву. Відносні розміри цих осей та значення кутів b (кут між віссю а і площиною течії) та g (кут зсуву,між гранями квадрата та ромба) характеризують величину деформації.
Згідно з цією моделлю визначають компоненти деформації (e) еліпсоїда по напрямках кожної осі за формулами:
ea=(a-d)/d, ec=(c-d)/d.
Дані за кількісними характеристиками зсувної деформації, розраховані на прикладі цієї моделі, наведено в шкалі тектонофацій (див табл. 3.4.1).
Дата добавления: 2015-04-07; просмотров: 1534;
