Связь дирекционных углов предыдущих и последующих линий.

Прямой результат измерений – когда после вычисления горизонтального угла β нельзя сразу перейти к вычислению прямоугольных координат, т.к. он является одной из полярных координат. Кроме того, β не является ориентирующим углом.

Т.к. дирекционный угол α стороны известен, то последовательно можно вычислить α всех сторон хода (см. рисунок).

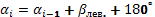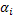Для левых углов формула связи: , где - дирекционный угол текущей стороны хода, 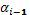- дирекционный угол предыдущей стороны хода, – измеренный левый горизонтальный угол по ходу между текущей и предыдущей сторонами.

Для правых: .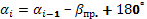

Если известны дирекционные углы сторон хода, то можно вычислить прямоугольные координаты вершин или точек хода, пользуясь измеренными линиями горизонтальных проложений.

§17 Кузнецова.

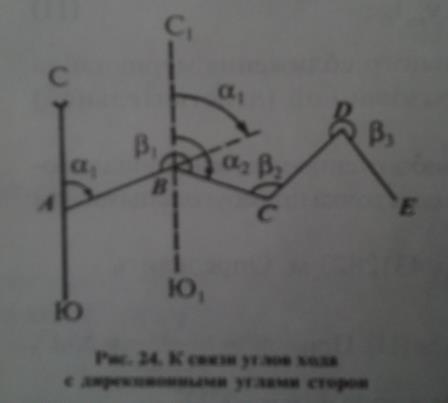
Пусть в ходе ABCDE дирекционный угол начальной линии АВ известен и равен 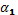. Требуется определить дирекционный угол 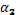последующей линии ВС, если в ходе измерены левые углы поворота 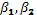и т.д.

Для решения в точке В проведём линию , параллельную СЮ, и, продолжив линию АВ, построим угол 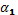при точке В. тогда из чертежа получим 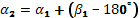(1).

Если в ходе измерены правые углы то .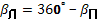

Подставив это выражение в (1), получим 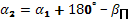(2).

По формулам (1) и (2) можно вычислить дирекционные углы всех линий хода.