Расчет объемов земляных работ по ЦМР

Расчет объемов по триангуляции Делоне

В задаче расчета объемов земляных работ в дополнение к существующей модели рельефа задается желаемая модель. Требуется рассчитать, какую территорию нужно срезать, а какую засыпать, чтобы получить желаемую поверхность. При этом нужно определить объемы перемещаемых масс грунта (сумма срезанного и засыпанного объемов) и балансовый объем (разница срезанного и засыпанного объемов, т.е. избыток или недостаток грунта). В наиболее простой постановке желаемая форма рельефа задается как некоторый регион на карте, в пределах которого требуется выравнивание поверхности под заданный горизонтальный уровень. Это применяется для оценки объемов работ при рытье котлованов с вертикальными стенками. Решение задачи с котлованом выполняется следующим образом.

Алгоритм расчета земляных работ при рытье котлована с вертикальными стенками и горизонтальным дном.

Шаг 1. Делается вырезка из общей триангуляции некоторой части по границе котлована. По сути, вначале делается копия исходной триангуляции и в неё вставляется граница котлована в качестве внешней границы триангуляции, т.е. все треугольники вне котлована отбрасываются.

Шаг 2. Вызывается алгоритм построения изоконтуров для вырезанной триангуляции на требуемом уровне дна котлована. Алгоритм возвратит два полигона, определяющих территории с излишком и с недостатком грунта соответственно.

Шаг 3. Для каждого треугольника вырезанной триангуляции выполняется сравнение с требуемым уровнем дна котлована. Если треугольник находится целиком выше дна, то его требуется засыпать, если целиком ниже – то срезать. Объем засыпки-срезки определяется как объем соответствующей треугольной призмы с двумя основаниями, одно из которых является текущим треугольником, а второе – проекцией этого треугольника на дно котлована.

Если треугольник пересекается с плоскостью дна котлована, то делается сечение треугольника на две части, для которых отдельно вычисляются объемы соответствующих призм. Конец алгоритма.

В более сложной постановке задачи расчета земляных работ требуемая поверхность задается как другая независимая триангуляционная модель. В такой форме задача возникает при проектировании вертикальной планировки территорий самого разного назначения.

Обычно эта задача решается на регулярных моделях с предварительным преобразованием исходных триангуляционных моделей. В явном же виде на триангуляции обычно эту задачу не решают, так как существующие для этого алгоритмы сложны и могут генерировать очень сложные полигоны, имеющие число точек, пропорциональное квадрату общего числа узлов в исходных триангуляциях. (рис. 9.4)

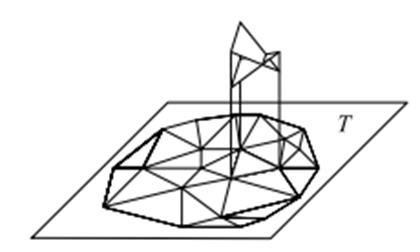
Рис. 9.4. Пересечение пространственных треугольников

В системе CREDO расчет объемов можно выполнять тремя способами:

1. по заданному контуру;

2. по сетке квадратов;

3. по трассе.

Рельеф в CREDO моделируется поверхностью, образованной гранями треугольников триангуляции Делоне. Методика расчета объемов в CREDO сводится к следующему:

каждая точка поверхности 1 проецируется на поверхность 2, а каждая точка поверхности 2 проецируется на поверхность 1. Для каждой пары таких точек определяется разность высот из моделей обеих поверхностей. Кроме того, такие пары формируются в каждой точке пересечения в плане ребер треугольников поверхностей 1 и 2. Таким образом, образуется набор точек, количество которых равно сумме количества точек поверхности 1 и 2, количества точек пересечения ребер треугольников. Каждая точка этого набора имеет значение разности отметок поверхностей 1 и 2. В слое «Объем» по всем этим точкам программа строит триангуляцию, образуя набор призм. Для каждой призмы рассчитывается объем, сумма всех объемов призм дает искомый объем. Собственно, описанная процедура значительно сложней, так как учитываются структурные линии, границы области расчета объемов, рассчитываются линии нулевых работ, объемы выемки, насыпи и т. д.

Таким образом, в ЦММ объемы с точки зрения математики по отношению к модели считаются абсолютно точно. Их точность по отношению к фактическому объему физических поверхностей зависит только от того, в какой мере сама съемка поверхности соответствует фактической. Для оценки точности расчета объемов выполнены специальные исследования, показавшие, что соблюдение нормативных требований к съемочным работам, точность расчета объемов для земляных работ находится в диапазоне 0,1–0,02; для асфальтобетонных покрытий, имеющих регулярную поверхность, точность расчета объемов на порядок выше.

Пример расчета приведен на рис. 9.5.

Рис. 9.5.

Рис. 9.6.

Расчет объемов по регулярной модели

Методы:

1. Трапецеидальный
2. Формула Симпсона
3. Формула 3/8 Симпсона
4. Другие

Все методы основаны на численном интегрировании. Различие- в аппроксимации подынтегральной функции (линейная, квадратическая, кубическая и т.д