Вращение – особая форма движения материи

Гравитация и космические системы

Настоящая статья является дальнейшим развитием теории вращающихся гравитационных полей в Космосе , изложенной в статьях «Гравитация в Космосе» .[ 1], «Природа гравитации и арифметика Космоса» [2] и «О гипотезе вращающейся гравитации во Вселенной» [3]. Одновременно эта статья является подведением итогов работы автора в изучении Космоса за период с 2001 по 3013 годы. Суть теории заключается в том, что все космические объекты в Космосе обладают вращающимися гравитационными полями, которые наводятся в объектах гравитационным полем ядра нашей Галактики. В статье «Гравитация в Космосе» в основном речь идет о вращении гравитационных полей внутри космического объекта: планеты, Солнца, ядра Галактики и почти ничего не говориться о свойствах гравитационных полей за пределами космического тела. Исключением является влияние гравитационных полей Солнца и Луны на гравитационное поле Земли. Настоящая статья касается космических систем: Солнечной, Галактической и Вселенной. Кроме того, в ней дан новый подход к теории вращения, к которому пришел автор в процессе изучения вращающихся гравитационных полей в Космосе.

Вращение – особая форма движения материи

Согласно первого закона Ньютона, при прямолинейном равномерном движении тела отсутствует ускорение [ 4]. При равномерном вращении тела вокруг своей оси, в нем возникают центробежные или центростремительные ускорения. Современная теория для объяснения вращательного движения использует векторное произведение, которое является объемной конструкцией и в принципе не может правильно отразить механизм вращения, т.к. при вращении векторы всех скоростей и ускорений находятся в одной плоскости. Именно по этой причине теория вращения не может объяснить природу центростремительных и центробежных ускорений. Этот пробел в теории вращения привел к ошибкам в изучении мира Космоса и мира Атома, а также в самой теории вращения.

Согласно современной теории вращающегося движения вектор угловой скорости и углового ускорения направлены вдоль оси вращения. Но, по второму закону Ньютона, вектор скорости и ускорения должен совпадать по направлению с вектором силы. В этом случае при ускоренном движении тело должно не увеличивать скорость вращения, а перемещаться вдоль оси с угловым ускорением.

Момент силы

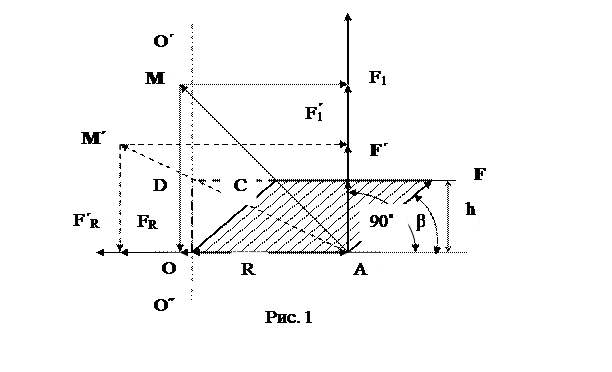
Ошибка современной теории вращательного движения заложена с объяснения момента силы для неподвижной точки и оси. В обоих случаях радиус рассматривается как вектор, хотя он не зависит от направления. Более правильно считать радиус плечом рычага, на который действует сила F чтобы повернуть радиус R относительно точки О (Рис.1). Точка О является центром, вокруг которого вращается радиус R под действием силы F. Все силы действуют в одной плоскости.

Рассмотрим простейший вариант: на радиус ОА= R исходящей из точки О, действует сила F под углом β, образованным продолжением радиуса и направлением вектора силы F (Рис.1) Модуль момента силы М равен площади параллелограмма OCFA со сторонами R и F. Вектор модуля силы лежит в плоскости параллелограмма и направлен из точки приложения сила А вдоль диагонали.. Вектор момента силы М меняет направление вместе с изменением направления силы F.

Площадь параллелограмма равна произведению основания R на высоту, а высота параллелограмма h =F·sinβ. Таким образом, модуль момента силы М= F·r·sinβ. (Рис.1). Проекция модуля момента силы на радиус дает нам силу AF_R действующую на точку А, вдоль радиуса. Проекция модуля М на перпендикуляр к радиусу в точке А дает нам силу AF, которая и обеспечивает поворот радиуса относительно точки О.

На Рис.1 дан еще один вариант определения момента силы М΄ для силы F΄ действующей на радиус R под углом 90˚.Модуль момента силы М΄ равен площади прямоугольника ODF΄A, который равен площади параллелограмма OCFA. Это означает, что модуль момента силы F равен модулю момента силы .F΄. Но на Рис.1 видно, что направление вектора М΄ изменилось по сравнению с вектором М_, что привело к уменьшению силы AF΄ по сравнению с AF. При этом уменьшение F₁F₁΄ точно равно силе F.Таким образом, сумма сил, действующих вдоль перпендикуляра к радиусу F΄+АF΄ = АF . Если модули векторов сил равны, то это означает, что на радиус R действуют одинаковые силы и данная система должна начать вращаться с одинаковой скоростью.

Проекция модуля момента силы на радиус указывает нам, что в момент начала вращения тела в нем возникают центростремительные силы, направленные вдоль радиуса к центру вращения. В принципе, это доказательство существования во вращательном движении центростремительного ускорения.

Момент сил относительно оси равен моменту сил относительно точки, т.к. ось должна проходить через неподвижную точку О перпендикулярно плоскости разложения сил, а саму ось можно представить как набор точек. Пересечение осью О΄О˝ плоскости разложения сил дает нам точку О, относительно которой и определен момент силы, представленный на Рис.1.

Момент количества движения (импульса)

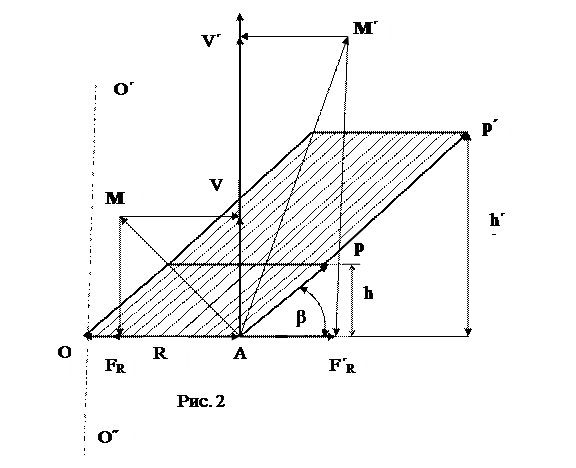
Учитывая, что радиус не вектор, мы получаем на Рис.2 аналогичную картину как на Рис.1. Различие между моментом силы и моментом импульса состоит в том, что сам импульс является произведением скаляра (массы) на вектор (скорость). На Рис.2 видно, что начиная с определенной скорости, проекция модуля импульса на радиус меняет направление, т.е. появятся центробежные силы. Более наглядно этот процесс представлен на графике изменения скорости и ускорения при равноускоренном вращательном движении(Рис.3).

Так как все силы действуют в одной плоскости, то момент импульса относительно оси равен моменту импульса относительно точки. Ось проходит через точку О перпендикулярно плоскости разложения сил (Рис.2).

На Рис.2 даны два варианта разложения сил: для импульса р и р΄, действующих на радиус под углом β, образованным импульсом и продолжением радиуса R. Проекция момента импульса М нарадиус R дает нам центростремительную силу AF_R, направленную вдоль радиуса к точке О или оси О΄О˝. А проекция момента импульса М΄ на радиус R дает нам центробежную силу AF΄_R , направленную вдоль продолжения радиуса от точки А.

Таким образом, анализ момента сил относительно точки и оси позволил объяснить природу центростремительных сил, возникающих при вращении тела. А определение момента импульса позволило показать, что при вращении тела, в зависимости от скорости, в нем возникают как центростремительные, так и центробежные силы. При этом все силы находятся п одной плоскости, перпендикулярной к оси вращения.

Линейные и угловые скорости и ускорения

Само понятие угловая скорость требует уточнения, как и понятие радиан. Под радианом понимается плоский угол, заключенный между радиусами окружности, длина дуги которой равна радиусу. Более правильно за радиан принимать не плоский угол, а саму дугу окружности, равную по длине радиусу окружности. В этом случае угловая скорость, измеряемая в рад/с, означала бы расстояние в радианах, которое точка, расположенная на поверхности тела, прошла по окружности за определенное время. Такой подход к угловой скорости позволяет однозначно решить проблему направления вектора угловой скорости и углового ускорения.

На Рис.3 дан «График изменения скорости и ускорения при равноускоренном вращательном движении». График построен на основании расчетов скоростей и ускорений для диска с радиусом 10м, который вращается с постоянным угловым ускорением 0,25 рад/с², начиная с нулевой скорости. График в оригинале выполнен в масштабе 1:100, что позволило сравнить действующие скорости и ускорения между собой.

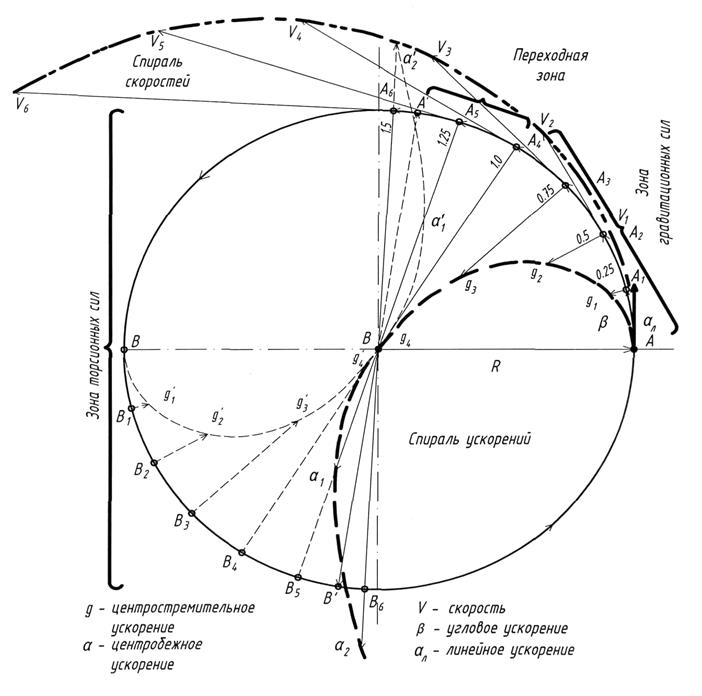
Рис.3

График изменения скорости и ускорения при равноускоренном

вращательном движении.

В расчетах применялись следующие формулы [ 4]:

g(a_цб) = v²/R (1)

где g – центростремительное ускорение [м/с²];

a_цб– центробежное ускорение [м/с²];

v – линейная скорость вращения [м/с];

R – радиус окружности /тела/ [м];

а_л = βR (2)

где а_л– линейное ускорение [м/с²];

β – угловое ускорение [рад/с²];

R – радиус окружности /тела/ [м].

ω_t = ω_o+ β t (3)

где ω_t – угловая скорость в момент времени t [рад/с];

ω_o –угловая скорость в момент времени t = 0 [рад/с];

β – угловое ускорение [рад/с²];

t –время вращения [с].

ω_s = ω₀·t±β t²/2 (4)

где ω_s - путь пройденный вдоль окружности /угловая координата/ за время t [рад];

ω₀ – угловая скорость в момент времени t = 0 [рад/с];

β – угловое ускорение [рад/с²];

t – время движения [с].

Согласно условию задачи, вращение тела началось с нулевой скорости, т.е. v_o=0 и ω_o=0 и с постоянным угловым ускорением равным 0,25 рад/с². В этом случае , согласно формуле (2), линейное ускорение а_л = 0,25·10 = 2,5 м/с². Но угловое ускорение 0,25 рад/с² для радиуса R =10м по окружности дает также величину 2,5 м/с², т.к. дуга АА₁ равна 2,5 м. Таким образом получаем, что модуль линейного ускорения равен вектору углового ускорения и лежит с ним в одной плоскости. Кроме того, вектор линейного ускорения направлен вдоль дуги окружности и начинается в точке А как и вектор линейной скорости.

При равноускоренном движении по окружности радиусом R, угловая скорость изменяется по формуле (3). Учитывая, что ω_о = 0, а β = 0,25 рад/с², через 4с угловая скорость в точке А₄ = 0,25·4 = 1,0 рад/с, а линейная скорость, согласно формуле (2) будет равна а_л = 1·10 =10 м/с (Рис.3). При этом длина дуги А₁А₂ А₃А₄ равна 10 м, т.е. модулю линейной скорости, а вектор угловой и линейной скоростей находятся в одной плоскости. Вектор угловой скорости, как и вектор углового ускорения, направлен вдоль дуги окружности. За 6с вращения в режиме равноускоренного движения, точка А пройдет по окружности, согласно формуле (4), расстояние равное 4,5 рад, т.е. повернется на угол 257,8˚.

.

Центростремительные и центробежные ускорения

Кроме графиков угловых и линейных скоростей и ускорений, на Рис.3 показано изменение нормальных ускорений а и g. Эти ускорения появляются под действием центростремительных или центробежных сил, возникающих при вращении тела. Причины возникновение этих сил показаны на Рис.2, при объяснении момента импульса. На Рис.3 показаны нормальные ускорения, рассчитанные по формуле (1) через каждую секунду (от 0 до 6с) для угловых скоростей от 0 до 1,5 рад/с. Как видно из графиков, при изменении угловой скорости от 0 рад/с до 1,0 рад/с ,происходит увеличение нормального ускорения g направленного к центру вращения. Максимальная величина центростремительного ускорения достигается при угловой скорости 1,0 рад/с. Дальнейшее увеличение скорости приводит к появлению центробежного ускорения (а₁,а₂), которое начинается от центра вращения и направлено вдоль радиуса (точнее, вдоль продолжения радиуса). Это ускорение при вращении тела с угловой скоростью от 1,0 рад/с до 1,41 рад/с полностью компенсирует центростремительное ускорение в пределах окружности (точка В΄). Точка В является симметричной к точке А, и при вращении в ней возникают симметричные ускорения как центростремительные, так и центробежные. В точках А΄ и В΄ происходит полная компенсация центростремительного ускорения. При дальнейшем увеличении скорости вращения за пределами тела действуют только центробежные ускорения. Подтверждением этого является изменение направления сил при увеличении импульса, представленные на Рис.2. При этом, как это видно на Рис.3, в точке А₆ действует центробежное ускорение точки В_6, а в точке В₆ – центробежное ускорение точки А₆.

Графики ускорений, представленные на Рис.3 позволяют наглядно оценить особенности предлагаемой теории вращения в познании законов Природы. В Космосе, где угловые скорости вращения составляют тысячные и миллионные доли рад/с, действуют только центростремительные ускорения и гравитационные поля. Они, как правило, связаны с огромными расстояниями и касаются планет, звезд, галактик и Вселенной. Границей перехода центростремительных ускорений в центробежные является угловая скорость в 1 рад/с , которая соответствует 1 обороту за 6,3 с. . Особенностью вращательного движения с угловой скоростью 1 рад/с является равенство линейной скорости радиусу объекта.

Угловые скорости свыше 1 рад/с широко применяются в производстве и ограничиваются прочностью материала, позволяющего выдерживать огромные центробежные силы.

Этим законам вращения подчиняется как вещество, так и поле, независимо от размера радиуса. Так, например, в атоме водорода, где мы имеем дело только с полем, электрон вращается вокруг протона с угловой скоростью 4,13414·10¹⁶рад/с. Это означает, что в атоме действуют только центробежные ускорения. Таким образом, новая теория вращения перекидывает мостик между миром Космоса и миром Атома. Вращающиеся поля в атоме и элементарных частицах называют торсионными полями (поля кручения) [5 ]. О связи Космоса с Атомом и роли торсионных полей – это тема для отдельной статьи. Но уже из выше сказанного видно, что законы вращения действуют как в мире Атома, так и в мире Космоса. Учитывая эту связь, предлагается все центробежные ускорения относить к торсионным силам, а центростремительные ускорения – к гравитационным силам (Рис,3).

При равноускоренном вращательном движении изменение вектора линейной скорости и вектора нормальных ускорений ( центростремительного и центробежного) происходит точно по закону спирали Архимеда. Это говорит о том, что спираль Архимеда является тем математическим аппаратом, который правильно отражает вращательное движение. В спирали Архимеда линейная и угловая скорости располагаются в одной плоскости.

Подводя итог всему выше сказанному, можно сделать следующие выводы:

1) Вращение – особая форма движения материи, которая создает в зависимости от скорости, вращения, центростремительные или центробежные ускорения. Законы вращения одинаково работают как для вещества, так и для поля.

2) Переход центростремительных ускорений в центробежные происходит при угловой скорости вращения равной 1 рад/с. При этой скорости вращения характерно равенство линейной скорости радиусу.

3) При вращении направления всех скоростей и ускорений находятся в одной плоскости. Вектор угловой скорости и ускорения направлен вдоль окружности и по модулю равен линейной скорости и ускорению.

4) Новая теория вращения позволяет перекинуть мостик от мира Космоса в мир Атома.