Переходная зона между плёнкой на поверхности твёрдого тела
и объёмной жидкостью и краевые углы
|
| |
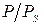 >0,95 понятие тонкой смачивающей плёнки и описывая их натяжение уравнением (54), Дерягин и Чураев рассматривают условия равновесия таких плёнок с объёмной жидкостью, например, каплей или вогнутым мениском. Условие их равновесия при этом подходе, как уже упоминалось. Определяется равенством расклинивающего давления в плёнке
>0,95 понятие тонкой смачивающей плёнки и описывая их натяжение уравнением (54), Дерягин и Чураев рассматривают условия равновесия таких плёнок с объёмной жидкостью, например, каплей или вогнутым мениском. Условие их равновесия при этом подходе, как уже упоминалось. Определяется равенством расклинивающего давления в плёнке 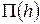 и перепада капиллярного давления
и перепада капиллярного давления 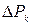 объёмной части жидкости (уравнение (55)).
объёмной части жидкости (уравнение (55)). 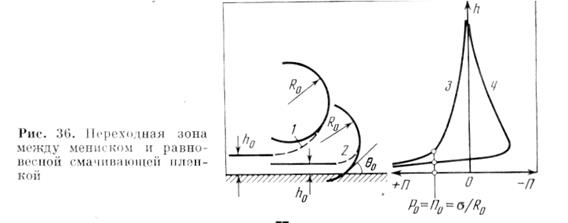
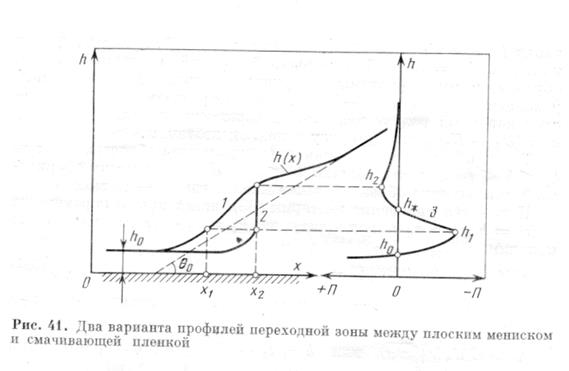
Плоская плёнка, находящаяся в сфере действия поверхностных сил подложки, не переходит прямо в объёмную жидкость. Между ними существует переходная зона, где ещё продолжается действие поверхностных сил. Дерягин и Чураев рассматривают два принципиальных случая переходной зоны: случай полного смачивания и случай неполного смачивания (рис.11). Первый случай (штриховая кривая 1) отвечает изотерме, показанной кривой 3. При этом продолжение невозмущённой кривой части мениска не пересекает поверхность подложки, краевой угол равен 0. Мениск посредством переходной зоны сообщается с плоской плёнкой толщиной 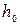 , отвечающей на изотерме
, отвечающей на изотерме 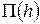 капиллярному давлению мениска
капиллярному давлению мениска 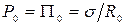 (для цилиндрической поверхности мениска). Во втором случае (кривая 2) продолжение невозмущённой части мениска образует с подложкой равновесный краевой угол
(для цилиндрической поверхности мениска). Во втором случае (кривая 2) продолжение невозмущённой части мениска образует с подложкой равновесный краевой угол 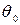 . Соответствующая изотерма
. Соответствующая изотерма 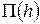 изображена кривой 4. Оба профиля переходной зоны построены на рис.11 для менисков одной и той же кривизны
изображена кривой 4. Оба профиля переходной зоны построены на рис.11 для менисков одной и той же кривизны 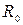 и соответственно для одного и того же давления
и соответственно для одного и того же давления 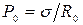 .
.
Поскольку в переходной зоне действуют и капиллярные и поверхностные силы, для нахождения зоны используется известное уравнение, выражающее постоянство химического потенциала молекул жидкости в слое переменной толщины 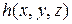 .
.
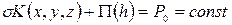 (61)
(61)
где 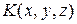 - локальное значение кривизны поверхности слоя.
- локальное значение кривизны поверхности слоя.
Уравнение (61) применимо для пологих профилей переходной зоны. Когда для описания действия поверхностных сил можно использовать изотермы плоских смачивающих плёнок 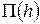 . В случае крутых профилей это приближение неприменимо, т.к. на состояние слоя с локальной толщиной
. В случае крутых профилей это приближение неприменимо, т.к. на состояние слоя с локальной толщиной
( 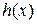 ) оказывают влияние также соседние участки твёрдой поверхности и жидкости.
) оказывают влияние также соседние участки твёрдой поверхности и жидкости.
|
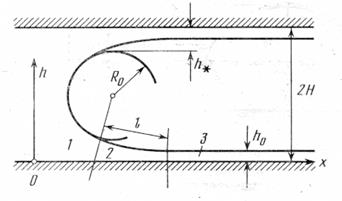
Уравнение (61) было применено для нахождения профилей переходной зоны в случае полного смачивания в плоской щели ширины Н (рис.12). Капиллярное давление мениска в такой щели 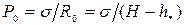 . Дерягин показал, что для изотерм типа
. Дерягин показал, что для изотерм типа 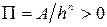 (А – константа Гамакера)
(А – константа Гамакера) 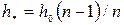 , где
, где  - показатель степени изотермы.
- показатель степени изотермы.
|
Для пологого профиля переходной зоны при 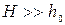 локальную кривизну поверхности жидкости можно выразить с помощью упрощения
локальную кривизну поверхности жидкости можно выразить с помощью упрощения  . Решение уравнения (61) для n=3 с учётом граничного условия
. Решение уравнения (61) для n=3 с учётом граничного условия 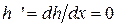 при
при 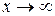 и условия сшивания переходной зоны с круговым мениском было получено Дерягиным, Старовым и Чураевым:
и условия сшивания переходной зоны с круговым мениском было получено Дерягиным, Старовым и Чураевым:
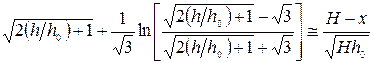 (62)
(62)
Расчёт на ЭВМ по уравнению (62) для плёнок неполярной жидкости показал, что длина переходной зоны растёт с увеличением ширины щели и соответственно с уменьшением кривизны поверхности мениска. Для случаев, когда объемная жидкость образует с плёнкой конечный краевой угол, расчёты переходной зоны осложняются. В этом случае пользуются упрощённым выражением для изотермы расклинивающего давления:
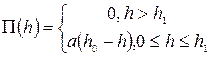 (63)
(63)
Вид этой изотермы, составленной из линейных участков, показан на рис.13,а. Эта изотерма отражает основные особенности реальных изотерм (рис.13,б), когда отсутствует β -часть изотермы.
Используя уравнение (61), были получены условия равновесия объёмной жидкости со смачивающей плёнкой, покрывающей плоскую подложку. Для цилиндрической поверхности объёмной жидкости, когда граница смачивания не искривлена, уравнение переходной зоны может быть записано в виде:
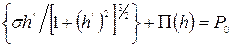 (64)
(64)
Рассматривается равновесие мениска в плоском капилляре шириной 2Н с покрывающими его поверхность плёнками. Капиллярное давление мениска равно (для случая ограниченного смачивания):
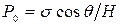 (65)
(65)
Граничными условиями уравнения (64) являются:
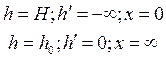
В результате интегрирования уравнения (64) с учётом условий (66) и (67) для Н много больше радиуса действия поверхностных сил получается выражение:
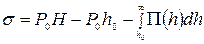 (68)
(68)
При замене Р0Н его значением из (65) окончательно получают:
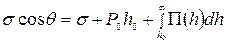 (69)
(69)
Уравнение равновесия (69) было получено также другим методом при использовании уравнения адсорбции Гиббса:
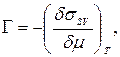 (70)
(70)
где Г (моль/см2) – адсорбция пара на подложке и 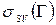 - межфазное натяжение твёрдой поверхности, покрытой адсорбционной плёнкой. Химический потенциал молекул адсорбата
- межфазное натяжение твёрдой поверхности, покрытой адсорбционной плёнкой. Химический потенциал молекул адсорбата 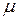 связан с относительным давлением его пара
связан с относительным давлением его пара 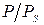 уравнением:
уравнением:
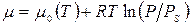 , (71)
, (71)
где 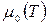 - химический потенциал объёмной фазы адсорбата при температуре Т.
- химический потенциал объёмной фазы адсорбата при температуре Т.
Интегрирование уравнения (70) при таком выборе постоянных интегрирования, чтобы при большой толщине адсорбционного слоя ( 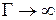 ) значения
) значения 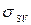 переходили в сумму межфазного натяжения твёрдое тело – жидкость (
переходили в сумму межфазного натяжения твёрдое тело – жидкость ( 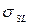 ) и поверхностного натяжения объёмной жидкости (
) и поверхностного натяжения объёмной жидкости ( 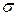 ), приводит к ур-ю:
), приводит к ур-ю:
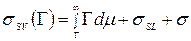 (72)
(72)
Подстановка выражения для 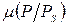 из (71) даёт:
из (71) даёт:
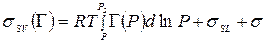 (73)
(73)
|
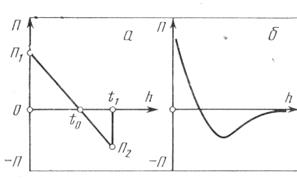
Используя экспериментальную изотерму расклинивающего давления воды на кварце (рис.14) в книге Дерягина и Чураева «Смачивающие плёнки» подробно рассматривается переходная зона на примере плоского мениска (  = 0). Как следует из уравнения (61), кривизна поверхности жидкости в переходной зоне (кривая 1) должна менять знак при такой толщине плёнки
= 0). Как следует из уравнения (61), кривизна поверхности жидкости в переходной зоне (кривая 1) должна менять знак при такой толщине плёнки 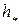 , когда меняет знак расклинивающее давление, т.е. при П = 0. При
, когда меняет знак расклинивающее давление, т.е. при П = 0. При 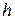 >
> 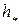 значение П > 0 , что означает К<0, т.е. существование выпуклой поверхности. При
значение П > 0 , что означает К<0, т.е. существование выпуклой поверхности. При 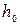 <
< 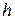 <
< 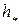 значения П < 0 и кривизна имеет обратный знак, т.е. поверхность этой части переходной зоны, показанной кривой 1, вогнута.
значения П < 0 и кривизна имеет обратный знак, т.е. поверхность этой части переходной зоны, показанной кривой 1, вогнута.
Такое рассмотрение показывает, что сосуществование 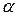 - и
- и 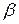 - плёнок возможно только при наличии выпуклой поверхности в области переходной зоны, т.е. только в случае неполного смачивания. Что касается вогнутости участка вблизи
- плёнок возможно только при наличии выпуклой поверхности в области переходной зоны, т.е. только в случае неполного смачивания. Что касается вогнутости участка вблизи 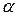 - плёнки, то здесь уместно вспомнить, что
- плёнки, то здесь уместно вспомнить, что 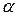 -
- 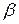 переход имеет качественный характер и использование общей изотермы расклинивающего давления для описания области перехода адсорбционной плёнки в тонкую смачивающую плёнку носит искусственный характер. Как считают Пригожин и Дефей, «уравнение состояние ван дер Ваальса можно использовать для приближённого описания изотерм реальных газов и жидкостей. В двухфазной системе оно приводит к изотермам… охватывающим области неустойчивых и метастабильных состояний» и «расчёт условий сосуществования фаз, основывающийся на использовании общего для них уравнения состояния и применение теоремы Максвелла, необходимо рассматривать как искусственный приём, который может привести к правильным результатам, но не может быть обоснован при последовательном статистическом рассмотрении». Необходимо напомнить также, что
переход имеет качественный характер и использование общей изотермы расклинивающего давления для описания области перехода адсорбционной плёнки в тонкую смачивающую плёнку носит искусственный характер. Как считают Пригожин и Дефей, «уравнение состояние ван дер Ваальса можно использовать для приближённого описания изотерм реальных газов и жидкостей. В двухфазной системе оно приводит к изотермам… охватывающим области неустойчивых и метастабильных состояний» и «расчёт условий сосуществования фаз, основывающийся на использовании общего для них уравнения состояния и применение теоремы Максвелла, необходимо рассматривать как искусственный приём, который может привести к правильным результатам, но не может быть обоснован при последовательном статистическом рассмотрении». Необходимо напомнить также, что 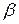 - часть изотермы расклинивающего давления можно получить только в условиях оттекания жидкости с поверхности твёрдого тела. При наличии трёхфазной границы только в условиях оттекания можно получить метастабильную тонкую смачивающую плёнку, Поэтому профиль переходной зоны, изображённый на рис.12, можно обнаружить только в случае оттекания. Хорошо известно, что
- часть изотермы расклинивающего давления можно получить только в условиях оттекания жидкости с поверхности твёрдого тела. При наличии трёхфазной границы только в условиях оттекания можно получить метастабильную тонкую смачивающую плёнку, Поэтому профиль переходной зоны, изображённый на рис.12, можно обнаружить только в случае оттекания. Хорошо известно, что 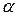 и
и 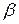 - плёнки воды значительно отличаются по свойствам. Применение уравнения (54) для описания натяжения
- плёнки воды значительно отличаются по свойствам. Применение уравнения (54) для описания натяжения 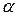 - плёнок очень условно. Как уже упоминалось, периметр смачивания, соответствующий вогнутой части кривой 1 рис.14, является закреплённым, его смещение связано со значительной энергией активации,
- плёнок очень условно. Как уже упоминалось, периметр смачивания, соответствующий вогнутой части кривой 1 рис.14, является закреплённым, его смещение связано со значительной энергией активации, 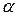 -
- 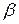 переход имеет характер фазового перехода, Поскольку многие свойства системы в этой области изменяются, едва ли можно говорить о конкретном профиле переходной зоны в этой области (начальном вогнутом участке кривой 1 на рис.14).
переход имеет характер фазового перехода, Поскольку многие свойства системы в этой области изменяются, едва ли можно говорить о конкретном профиле переходной зоны в этой области (начальном вогнутом участке кривой 1 на рис.14).
Таким образом, отдавая должное достижениям концепции Дерягина для описания устойчивости смачивающих плёнок, а в связи с этим и феномена угла оттекания, использование этой теории для рассмотрения конечных равновесного краевого угла и угла натекания для гидрофильных твёрдых тел является, по нашему мнению, неплодотворным.
Дата добавления: 2015-04-05; просмотров: 1231;
