Решение дифференциальных уравнений

Дифференциальные уравнения представляют собой функцию вида:

y'=f(x,y)

Решить дифференциальное уравнение – это, значит найти очередную точку кривой, которая описывается этим уравнением.

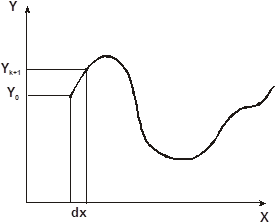
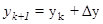– каждое новое значение будет равно: предыдущее (y_k) + добавка .

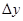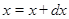
Задача:

Решить дифференциальное уравнение:

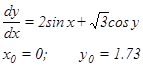
на отрезке от х=0 до х=1.5 с шагом 0.1 по методу Рунге-Кутта 4 порядка:

.

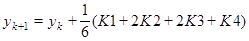
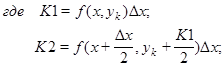
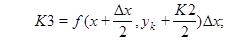
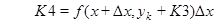Решение:

Необходимо в программе задать цикл вычисления, при котором на каждом цикле будут вычисляться значения коэффициентов K1,K2,K3,K4 и значения y.

WRITE (6,*)’ Введите ИД: Xo,Yo,DX,Xкон’

READ (5,*) X0,Y0,DX,XK

Y=Y0

C Задаём цикл

DO 1 X=X0,XK,DX

AK1=FUN(X,Y)*DX

Коэффициенты К1, К2, К3, К4 заменены на AK1, AK2, AK3,AK4 потому, что первый символ (буква K) относит переменную к целому типу (I, J, K, L, M, N), а она должна быть вещественного типа. Fun – подпрограмма функция, описывающая наше уравнение.

AK2=FUN(X+DX/2.,Y+AK1/2.)*DX

AK3=FUN(X+DX/2.,Y+AK2/2.)*DX

AK4=FUN(X+DX,Y+AK3)*DX

Y=Y+(AK1+2.*AK2+2.*AK3+AK4)/6.

XN=X+DXЧтобы напечатать X, соответствующее новому значению Y

1 WRITE (6,*) ’При X=’,XN,’ Новое значение Y=’,Y,

PAUSE

STOP

END