С Программа №8.

С Вычисление определённого интеграла по методу прямоугольников

1 WRITE(6,*)’Введите значения A,B,DX’

READ(5,*) A,B,DX

C Вычисляем количество точек на кривой

N=(B-A)/DX+1

DX=(B-A)/(N-1)

C Вычисление суммы

F=0.

Как всегда, перед вычислением суммы обнуляем ячейку памяти

DO 2 X=A,B–DX,DX

Конечное значение цикла берём равным B-DX для того, чтобы не вычислить большую площадь, т.к. после окончания цикла переменная цикла имеет значение, которое больше конечного значения цикла на величину шагаDX.

PAUSE

GO TO 1

STOP

END

Оператором цикла DO переменной цикла X присваивается начальное значение A. Организуются циклические вычисления в области цикла, включая оператор с меткой 2. На каждом новом цикле значение X увеличивается на величину шага DX. В области цикла сначала вычисляется значение функции FX,а затем к переменнойF,в которой накапливается сумма значений локальных интегралов, прибавляется значение функции, умноженное на DX. Вычисления будут проводиться до достижения переменной цикла X значения B-DX. В последний раз к Fприбавится FX*DX (последняя площадка) и в области цикла вычисления завершатся.

Чем меньше величина шага DX, тем выше точность вычисления интеграла.

Задача 2:

Вычислить значение предыдущего интеграла, методом трапеции, который более точный.

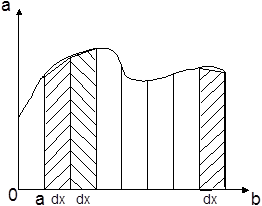
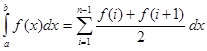
Решение:

1.Вычислим все значения функции F(x) и запомним их в массиве.

2.Распечатаем все значения функции при соответствующем аргументе.

3.Вычислим значение суммы для получения значения интеграла по методу трапеции.