Особенности измерения температуры

Почти во всех методах измерения температуры чувствительный элемент приводится в соприкосновение со средой, в которой необходимо измерять температуру. При этом температура чувствительного элемента должна быть равна или пропорциональна температуре среды. Совпадение этих температур зависит от многих факторов, в том числе от размеров, формы и материала чувствительного элемента, от размеров, формы и материала контролируемой среды и от условий передачи теплоты к чувствительному элементу. Всякий чувствительный элемент, внесенный в контролируемую среду, искажает ее температурное поле, что является одной из причин несовпадения температур. С другой стороны, температура чувствительного элемента тем ближе к температуре среды, чем лучше теплообмен между средой и чувствительным элементом.

Передача теплоты к чувствительному элементу термометра может происходить через конвекцию, лучеиспускание и теплопроводность. Теплообмен через конвекцию имеет место при измерении температуры жидкости и газов. Если среда, в которой измеряется температура, ограничена стенками, то вследствие прозрачности жидкости и газов теплообмен между стенками и чувствительным элементом будет происходить также и через лучеиспускание. Наконец, при измерении температуры твердых тел передача теплоты к чувствительному элементу происходит в основном через теплопроводность.

Количественные характеристики теплообмена между средой с температурой q₀ (илиТс - абсолютной температурой стенки) и чувствительным элементом с температурой q(или Т) конвекцией, излучением или теплопроводностью определяются формулами:

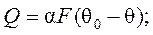
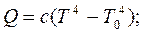
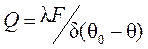, (6.3)

где α – коэффициент конвективного теплоперехода, зависящий от скорости обтекания чувствительного элемента и меняющийся от 3·10^-7 до 5·10^-5 Дж/см ^оС; F–площадь соприкосновения чувствительного элемента со средой; с – коэффициент теплоизлучения, равный для абсолютного черного тела 5,709·10^-7 Дж/см^{2 0}К⁴; λ– коэффициент теплопроводимости; d– толщина тонкого слоя, отделяющего чувствительный элемент от твердой стенки, температуру которой измеряют.

Из выражений (6.3) видно, что для улучшения теплообмена между средой и чувствительным элементом необходимо увеличивать площадь соприкосновения F, а при измерении температуры газов и жидкостей следует увеличивать коэффициент теплопередачи aпутем увеличения скорости обдувания.

При измерении температуры газов, движущихся с большими скоростями, особое значение приобретает переход кинетической энергии газов в тепловую энергию в местах торможения потока. Известно, что если q_Т – температура затормороженного потока и q_С – статическая температура, которая была бы замерена прибором, движущимся вместе с газом со скоростью V, то имеет место соотношение:

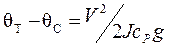, (6.4)

где J– механический эквивалент тепла; c_р -теплоемкость при постоянном давлении; g-ускорение силы тяжести.

Из соотношения (6.4) видно, что чем больше скорость движения, тем больше разность q_Т- q_С. При V=300 м/с эта разность составляет 44 °С.

В газотурбинных двигателях и наружном воздухе измеряют температуру заторможенного потока, для чего чувствительный элемент помещают в пространство с почти полным торможением. Но при этом уменьшается интенсивность теплообмена, поэтому в приборах, измеряющих температуру заторможенного потока, динамические погрешности больше, чем в приборах, измеряющих статическую температуру.

Под динамической погрешностью термометра следует понимать запаздывание в показаниях, вызванное конечной скоростью передачи тепла от контролируемой среды к чувствительному элементу. Динамические погрешности определяются не только свойствами прибора, но и скоростью изменения измеряемой температуры. Эти погрешности тем больше, чем больше скорость изменения температуры.

Для оценки динамических погрешностей предположим, что теплочувствительный элемент представляет собой однородное тело плотностью r, объемом uи соприкасается с контролируемой средой поверхностью F. Температура qпо теплочувствительному элементу распределена равномерно.

Количество тепла, переданное от среды к чувствительному элементу за время Dt, равно:

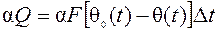, (6.5)

где a– коэффициент теплопередачи.

Это же количество тепло можно выразить через повышение температуры элемента:

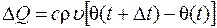, 6.6)

где с -удельная теплоемкость материала чувствительного элемента.

Разлагая член q(t+ ∆t)в рядТейлора и ограничиваясь линейным членом, получим вместо (6.6):

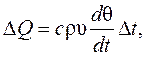(6.7)

Приравнивая выражения (6.7) и (6.6), найдем

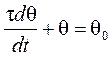(6.8)

где t– постоянная временная чувствительного элемента.

, (6.9)

где m– масса чувствительного элемента.

Решение уравнения (6.8) при скачкообразном изменении температуры от 0 до q₀можно представить в виде:

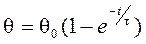.(6.10)

На рисунке 6.1 приведены кривые, показывающие характер нарастания температуры чувствительного элемента при различных значениях отношения t/t.

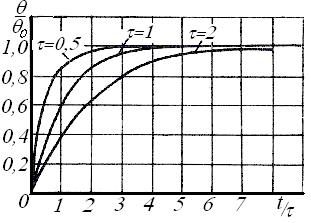
Рис. 6.1. Переходная функция термочувствительного элемента

Видно, что с увеличением tнарастание температуры замедляется. Для уменьшения постоянной времени tнеобходимо уменьшать объем uи теплоемкость с чувствительного элемента и увеличивать поверхность соприкосновения Fи коэффициент теплоотдачи α.

При заданных конструктивных размерах чувствительного элемента постоянная времени зависит от весового расхода газа, омывающего чувствительный элемент. Если G₁и G₂ – весовые расходы газов в единицу времени, а t₁и t₂– соответствующие постоянные времени, то имеет место соотношение:

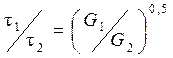(6.11)

Отсюда следует, что с подъемом на высоту весовой расход газов уменьшается, что приводит к возрастанию постоянной времени теплочувствительного элемента.