Методика расчёта трубопровода с параллельным соединением

Сложными трубопроводами называют разомкнутые или замкнутые сети, часто с уравнительными резервуарами, тешюобменными или другими аппарата­ми. Характерной особенностью сложного трубопровода является наличие раз­ветвлённых и параллельных участков. Гидравлический расчёт таких сетей с учё­том меняющегося во времени расхода в соответствии с производственными тре­бованиями эксплуатации той или иной системы представляет очень сложную за­дачу, такие расчёты рассматриваются в специальных курсах (водоснабжение, вен­тиляция, отопление и др.).

Из всех возможных схем сложных трубопроводов в данной работе рассмат­ривается параллельное соединение - случай, когда трубопровод в некоторой точке разветвляется на несколько труб, которые затем вновь соединяются в одной точке; массовый расход G₀ общего трубопровода до деления и после объединения труб, очевидно, один и тот же . Для упрощения расчётов рассматриваем изотер­мическое течение несжимаемой жидкости (газа).

Основной задачей при расчёте трубопровода с параллельным соединением является определение расходов G₁,G₂...G_nв параллельных ветвях трубопрово­да и перепада давления между точками разветвления и соединения труб дрг (по­следнее необходимо для расчёта мощности насоса или вентилятора), если извест­ны общий расход G₀и конструктивные характеристики трубопроводов.

Суммарные потери давления при движении жидкости (газа) для каждой па­раллельной ветви одинаковы и складываются из потерь давления на трение Δр_тр и потерь на местные сопротивления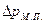

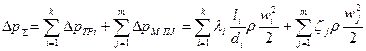, (36)

где 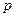— плотность жидкости;

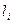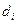и — длина и диаметр 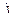-го участка трубопровода;

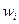— коэффициент гидравлического трения 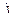-го участка трубопровода;

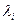— средняя скорость в 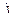-ом сечении трубопровода;

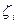— коэффициент местного сопротивления;

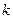— число участков трубопровода одинакового диаметра;

т — число местных сопротивлений.

Если скорость в соответствующих сечениях трубопровода выразить через массовый расход 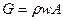, который для каждой ветви постоянен, то уравнение (36) для первой ветви с учетом

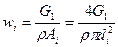и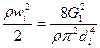

запишется в виде:

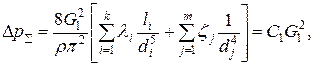(37)

где

.

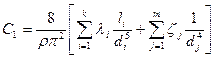Аналогично можно записать потери давления для других ветвей

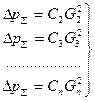. (38)

Так получаются п уравнений (по числу веток трубопровода). Но в этих урав­нениях число неизвестных равняется п + 1: это искомые расходы и потерянное давление Δр_Σ. Следовательно, система (38) должна быть дополнена ещё одним уравнением. Таким недостающим уравнением будет уравнение расходов:

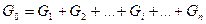. (39)

Решая совместно систему (38) с (37), выражаем расходы во всех ветвях через расход в первой ветви G₁:.

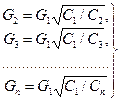(40)

Делая подстановку в уравнение (39), получим

_.

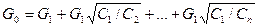Откуда расход в первой ветви

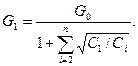
После этого из (40) можно определить последовательно расходы в других ветвях

_.

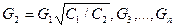Потерянное давление определяем по одному из уравнений системы (38)

.

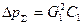Приведённое решение предполагает. квадратичный закон сопротивлений, ко­гда потери не зависят от числа Рейнольдса.

Для проверки этого предположения определяются числа Rе для каждого тру­бопровода по формуле

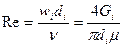, (41)

где ν и μ — кинематическая и динамическая вязкости (μ=νρ).

По найденным числам Рейнольдса уточняются все коэффициенты гидравлического трения λ'_i, коэффициенты местных сопротивлений ζ'_jи по ним уточня­ются значения коэффициентов С'₁,C'₂...С'_n. Повторяя расчёт аналогично ука­занному выше, но при уточнённых коэффициентах С'₁,С'₂...С'_n определяется уточнённый массовый расход для первой ветви

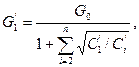
а затем через него для остальных ветвей 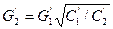и т. д.

При необходимости можно внести дальнейшее уточнение повторным аналогичным расчётом.

Потерянное давление между точками разветвления и соединения труб

.

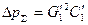После определения потерь давления определяется мощность насоса, необхо­димая для прокачки жидкости, по формуле

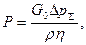(42)

где 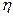- к. п. д. насоса.