Методика термодинамического расчета

Математическое моделирование идеализированного цикла поршневого ДВС со смешанным процессом подвода тепловой энергии и с политропными процессами сжатия и расширения рабочего тела

Методика термодинамического расчета

3.1. Исходные данные

Рабочее тело — воздух, подчиняющийся законам идеального газа.

Давление рабочего тела в исходной точке “a” (начало процесса политропного сжатия) – Pа (рис. 1).

Температура рабочего тела в исходной точке - Tа.

Максимальный объем рабочего тела (полный объем цилиндра) - Vа.

Степень сжатия - ε — Vа/Vс (Vс –наименьший объём рабочего тела после политропного сжатия).

Степень повышения давления рабочего тела в изохорном процессе подвода тепловой энергии λ = Pу/Pс = Pz/Pc (Pс, Ру и Pz - давление рабочего тела в характерных точках цикла – см. рис.1).

Cтепень предварительного расширения рабочего тела в изобарном процессе подвода тепловой энергии к рабочему телу - ρ = Vz/Vс.

Показатель политропы сжатия рабочего тела (воздуха) –n1.

Показатель политропы расширения рабочего тела – n2.

Частота вращения коленчатого вала двигателя —N.

Число цилиндров в двигателе — i.

Тактность двигателя принята равной четырём.

.

3.2. Краткое описание идеализированного цикла теплового двигателя

с изохорно-изобарным процессом подвода энергии в тепловой форме

и с политропными процессами сжатия и расширения рабочего тела

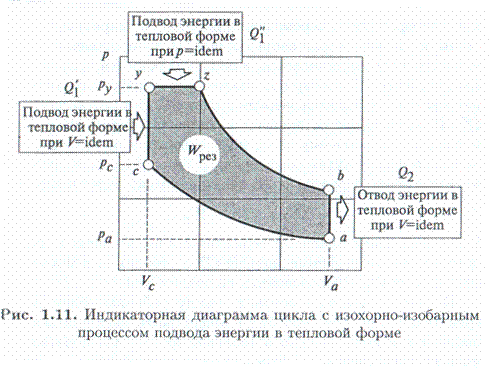
Индикаторная диаграмма такого цикла показана на рис.1.

Важные особенности рассчитываемого цикла - цикл замкнутый и рабочее тело цикла ни в одном термодинамическом процессе, составляющем цикл, не обменивается веществом с окружающей средой.

Первая особенность, в соответствии со вторым законом термодинамики, является признаком возможности создать на основе такого цикла двигатель, непрерывно и длительно производящий механическую работу. Такая возможность существует благодаря тому, что в замкнутом цикле параметры состояния рабочего тела периодически возвращаются к одним и тем же значениям в любой точке цикла, условно принятой в качестве начальной.

Вторая особенность позволяет рассчитывать работу рабочего тела во всех термодинамических процессах на основе уравнений, описывающих работу изменения объёма, которая осуществляется при расширении или сжатии рабочего тела под поршнем теплового двигателя.

Рассчитываемый цикл состоит из следующих термодинамических процессов (рис.1.):

· политропный процесс сжатия а-с рабочего тела;

· изохорный процесс подвода теплоты к рабочему телу с-y;

· изобарный процесс подвода теплоты к рабочему телу y-z;

· политропный процесс расширения z-b рабочего тела;

· изохорный процесс отвода теплоты от рабочего тела b-а.

3.2.1. Термодинамический процесс политропного сжатия рабочего тела. Уравнения обмена механической и тепловой энергией между рабочим телом и окружающей средой. Энтропия рабочего тела

В термодинамическом процессе a-с рабочее тело сжимается политропно. Это означает, что рабочему телу передается энергия в механической форме (путем совершения над ним работы сжатия Wa-c). Работу сжатия над рабочим телом совершает окружающая среда, например маховик двигателя, посредством перемещения поршня двигателя. В соответствии с правилом знаков, принятым в термодинамике, эта работа отрицательна.

В политропном процессе сжатия а-с рабочее тело обменивается энергией с окружающей средой и в тепловой форме. В начале процесса сжатия стенки цилиндра двигателя, как правило, имеют температуру более высокую чем температура рабочего тела и, следовательно, к рабочему телу подводится теплота. В конце процесса сжатия наоборот-рабочее тело имеет более высокую температуру нежели стенки цилиндра. В этой части процесса сжатия тепло отводится от рабочего тела. В целом, за весь процесс сжатия знак тепловой энергии, которой рабочее тело обменивается с окружающей средой, может быть как положительным, так и отрицательным. Подробнее о знаке тепловой энергии в политропных процессах написано далее.

3.2.1.1. Уравнение термодинамического политропного процесса сжатия [1]

По определению

P*V ⁿ¹ = const, где n1 – показатель политропы 3.1

Запишем также и уравнение состояния идеального газа

P*V = (M/µ)*R*T = Nмол* R*T 3.2

Здесь:

М– масса газа (рабочего тела);

µ - молекулярная масса газа;

R = 8,314 Дж/(моль*K) – универсальная газовая постоянная;

Nмол – количество молей газа.

Используя эти уравнения, можно записать и другие удобные соотношения для расчёта параметров рабочего тела в процессе политропного сжатия.

T*V ^{(n1 – 1)} = const 3.3

T =const*P^{(n1 -1)/n1}3.4

3.2.1.2. Энергия в механической форме, которой обмениваются рабочее тело и окружающая среда (в нашем случае это работа изменения объёма), описывается интегральным соотношением [1]

W = ∫PdV 3.5

После интегрирования в полученное выражение необходимо подставить пределы интегрирования – параметры состояния рабочего тела, соответствующие началу и концу термодинамического процесса.

Операцию интегрирования можно произвести после подстановки под знак интеграла зависимость давления рабочего тела от его объёма в каком-либо термодинамическом процессе. Можно поступить и наоборот - подставить под знак интеграла зависимость объёма рабочего тела от его давления.

В случае, когда необходимо рассчитать работу рабочего тела в политропном процессе, можно использовать зависимость 3.1.

Так как в исходных данных задано постоянное значение показателя политропы, то интегрирование сводится к нахождению табличного интеграла, и в итоге получаем зависимость для работы изменения объёма в процессе сжатия рабочего тела

Wa-c = (Ра*Vа – Pс*Vс)/(n1-1) 3.6

В этой зависимости:

Wa-c – механическая работа рабочего тела в политропном процессе;

индексы «а» и «с» при параметрах состояния рабочего тела относятся к началу и концу термодинамического сжатия соответственно.

В процессе политропного сжатия температура рабочего тела увеличивается и, в соответствии с уравнением состояния идеального газа, увеличивается и значение P*V. В термодинамическом процессе политропного расширения рабочего тела значение P*V уменьшается. Таким образом, отрицательный знак механической работы в процессе сжатия (уравнение 3.6) соответствует правилу знаков термодинамики.

3.2.1.3. Энергия в тепловой форме, которой обмениваются рабочее тело и окружающая среда в любом термодинамическом процессе может быть получена из определения теплоёмкости рабочего тела в термодинамическом процессе. В дифференциальной форме определение теплоёмкости рабочего тела имеет вид

dq_x = MCx*dT 3.7

В этой зависимости

T– температура рабочего тела;

q_x – удельная тепловая энергия, которой обмениваются 1 моль рабочего тела и окружающая среда в произвольном термодинамическом процессе;

МСx – мольная теплоёмкость рабочего тела произвольного термодинамического процесса (на это указывает);

индекс «x»указывает на то, что параметры с этим индексом относятся к произвольному термодинамическому процессу.

Соотношение 3.7 следует понимать так: каждому термодинамическому процессу соответствует своё значение мольной теплоёмкости рабочего тела (иначе говоря, теплоёмкость – функция процесса).

Понятно, что непосредственное использование уравнения 3.7 возможно лишь в случае, когда известна зависимость для удельной мольной теплоёмкости рабочего тела в рассматриваемом термодинамическом процессе.

Такая зависимость для политропного процесса может быть получена из уравнения первого начала термодинамики [1 - 3]

dq_x = MCv*dT + W, 3.8

в котором

MCv – мольная теплоёмкость рабочего тела в изохорном процессе (справочная величина [2]);

W – удельная работа рабочего тела (работа 1 моля вещества) в рассматриваемом термодинамическом процессе.

Дополняя последнее уравнение зависимостью 3.6 при постоянном показателе политропы, получим удельную мольную теплоёмкость политропного процесса

MCп = MCv*(n1-k)/(n1-1), 3.9

где

MCп - мольная теплоёмкость политропного процесса;

k– показатель адиабаты, который равен отношению удельной мольной теплоёмкости газа в процессе с подводом теплоты при постоянном объёме к удельной мольной теплоёмкости при подводе теплоты при постоянном объёме газа.

Тогда, из последнего уравнения и уравнения 3.7 следует: удельная энергия в тепловой форме, которой обмениваются рабочее тело и окружающая среда в политропном процессе, может быть определена по соотношению

q_п = MCп*(Tk – Ts), 3.10

в котором

Tk и Ts – значения температур рабочего тела в конце и в начале политропного процесса соответственно.

Выполним анализ уравнений 3.9 и 3.10. В тепловых двигателях затраты механической энергии на процесс сжатия значительно больше, чем обмен теплотой между рабочим телом и окружающей средой. Тогда, из уравнения 3.8 следует, что в процессе сжатия температура рабочего тела увеличивается.

Из уравнения 3.10 видно, что при увеличении температуры рабочего тела теплота в процессе подводится в случае, когда удельная мольная теплоёмкость MCп > 0. Этому требованию удовлетворяет условие n1 > k(см. уравнение 3.9). И наоборот, в процессе политропного сжатия, если показатель политропы меньше показателя адиабаты (n1 < k) теплота отводится от рабочего тела в окружающую среду (q < 0).

Аналогичное исследование можно выполнить и для термодинамического процесса политропного расширения. В таком процессе температура рабочего тела уменьшается. Тогда, если показатель политропы меньше показателя адиабаты (n2 < k), теплота подводится к рабочему телу от окружающей среды (q > 0). Когда в процессе политропного расширения показатель политропы больше показателя адиабаты (n2 > k), теплота отводится от рабочего тела в окружающую среду (q < 0).

И наконец, если показатель политропы равен показателю адиабаты, т.е. если осуществляется адиабатический процесс сжатия или расширения, то рабочее тело не обменивается энергией в тепловой форме с окружающей средой. Последний вывод соответствует определению изоэнтропийного процесса.

3.2.2. Термодинамический изохорный процесс подвода тепловой энергии

В термодинамическом изохорном процессе c-y (рис.1) энергия в тепловой форме подводится к рабочему телу. Подвод энергии в этом процессе в двигателях внутреннего сгорания происходит в результате окисления (горения) топлива. Горение топлива происходит настолько быстро, что его большая часть сгорает при весьма малых перемещениях поршня. Это обстоятельство и позволяет рассматривать этот процесс как изохорный.

Из условия V = const (по определению изохорного процесса) и из уравнения состояния идеального газа 3.2 следует

P = const*T 3.11

Эта зависимость позволяет определять параметры состояния рабочего тела в изохорном процессе.

Из определения работы изменения объёма (уравнение 3.5) следует, что в изохорном процессе рабочее тело не обменивается энергией в механической форме с окружающей средой. Действительно, в изохорном процессе поршень расширительной машины неподвижен и, значит, рабочее тело не совершает механическую работу и над рабочим телом не совершается работа изменения объёма.

Wc-y = 0 3.12

Обмен энергией между рабочим телом и окружающей средой в тепловой форме в изохорном термодинамическом процессе может быть рассчитан непосредственно из определения теплоёмкости рабочего тела – уравнение 3.7. Для изохорного процесса это уравнение принимает вид

dq_v = MCv*dT.

Интегрируя это уравнение при постоянном значении мольной теплоёмкости газа, получим

q_v = MCv*(Tk - Ts) 3.13

3.2.3. Термодинамический изобарный процесс подвода тепловой энергии

В изохорном процессе с-y топливо сгорает не полностью; часть топлива сгорает при перемещающемся вниз от верхней мёртвой точки поршне. В термодинамическом изобарном процессе y-z (рис.1) энергия в тепловой форме подводится к рабочему телу именно в результате догорания части не сгоревшего ранее топлива.

Из условия P = const (по определению изобарного процесса) и из уравнения состояния идеального газа 3.2 следует

V = const*T 3.14

Эта зависимость позволяет определять параметры состояния рабочего тела в изобарном процессе.

Из определения работы изменения объёма (уравнение 3.5) для изобарного процесса может быть получено

Wy-z = Pz*(Vz - Vy), 3.15

где

Wy-z - энергия в механической форме, которую рабочее тело отдаёт окружающей среде в термодинамическом изобарном процессе расширения рабочего тела при подводе теплоты. Иными словами – это работа, совершаемая рабочим телом. Знак этой работы положителен, т.к. в этом процессе поршень перемещается вниз от верхней мёртвой точки и объём рабочего тела увеличивается - Vz > Vy (см. рис.1). Это соответствует правилу знаков термодинамики;

P – давление рабочего тела в изобарном процессе y-z.

Vz и Vy - конечное и начальное значения объёма рабочего тела в изобарном процессе y-z.

Обмен энергией между рабочим телом и окружающей средой в тепловой форме в изобарном термодинамическом процессе может быть рассчитан непосредственно из определения теплоёмкости рабочего тела – уравнение 3.7. Для изобарного процесса это уравнение принимает вид

q_p = MCp*dT,

где

MCp – мольная теплоёмкость в термодинамическом процессе при постоянном давлении. MCp – это справочная величина.

Интегрируя это уравнение при постоянном значении мольной теплоёмкости газа, получим

q_p = MCp*(Tz - Ty) 3.16

3.2.4. Термодинамический процесс политропного расширения рабочего тела

В термодинамическом процессе z-b происходит политропное расширение рабочего тела. Объём рабочего тела в конце процесса расширения принимает начальное значение (см. рис.1) - Vb = Va.

Политропный процесс сжатия достаточно подробно описан в разделе 3.2.1. Уравнения политропных процессов расширения и сжатия идентичны и поэтому вывод уравнений для политропного процесса расширения здесь не приводится.

Однако, следует иметь в виду, что в политропном процессе расширения рабочего тела последнее совершает механическую работу над окружающей средой, и эта работа, в соответствии с правилом знаков термодинамики, положительна.

Ещё одна особенность политропного расширения рабочего тела в ДВС состоит в следующем. В процессе расширения рабочее тело имеет более высокую температуру, нежели стенки цилиндра двигателя. Поэтому тепловая энергия отводится от рабочего тела в окружающую среду. Вместе с тем, в этом процессе догорает оставшееся топливо и к рабочему телу продолжает подводиться тепло. В общем случае знак тепловой энергии, которой рабочее тело обменивается с окружающей средой, может быть как положительным, так и отрицательным. Как было отмечено ранее, знак тепловой энергии в политропном процессе расширения зависит от соотношения между показателями политропы и адиабаты. Заданное в исходных данных к контрольной работе значение показателя политропы учитывает оба отмеченных явления.

3.2.5. Термодинамический изохорный процесс отвода тепловой энергии

от рабочего тела

В термодинамическом процессе b-a происходит изохорный отвод теплоты от рабочего тела. В поршневых двигателях внутреннего сгорания этот резкого уменьшения давления рабочего тела при открытии выпускных клапанов двигателя. Давление, температура и энтропия рабочего тела в конце этого процесса принимают те же значения, которые рабочее тело имело в начальной точке.

В целом, уравнения для изохорного процесса отвода тепла полностью аналогичны уравнениям изохорного процесса подвода тепла и поэтому для описания изохорного процесса b-a следует пользоваться уравнениями раздела 3.2.2.