Дроссели переменного тока

Дроссель переменного тока состоит из замкнутого магнитопровода и обмотки, которая включается в цепь переменного тока последовательно с нагрузкой. Пусть к зажимам ab приложено синусоидальное напряжение, которое изменяется по закону:

u_сети=U_m·sin(wt+y), (7.1)

где, U_m – амплитудное значение напряжения;

w – круговая частота;

y – начальная фаза.

График функции u_сети=f(wt) изображён на рисунке 7.1.

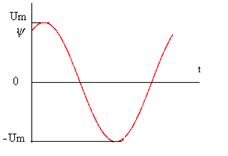
Рисунок 7.1 График функции u_сети=f(wt)

При приложении к зажимам цепи синусоидального напряжения в цепи потечёт ток i₀. Этот ток создаёт магнитный поток Ф₀, который, пронизывая магнитопровод, и создаёт в обмотке дросселя переменного тока электродвижущую силу (ЭДС) е. При синусоидальной форме кривой питающего напряжения действующее значение ЭДС будет равно:

Е=4·k_ф·W·f·Ф_m, (7.2)

где W – число витков обмотки дросселя;

f – частота;

Ф_m – амплитудное значение магнитного потока;

k_ф – коэффициент формы кривой питающего напряжения.

Для синусоидального тока коэффициент формы равен:

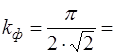1,11.

С учётом этого действующее значение ЭДС равно:

Е=4,44·W·f·Ф_m. (7.3)

Максимальное значение магнитного потока равно:

Ф_m=В_m·S, (7.4)

где B_m – максимальная индукция в сечении сердечника;

S – площадь сечения сердечника.

С учётом формул (12.3) и (12.4) получим:

Е=4,44·W·f·B_m·S. (7.5)

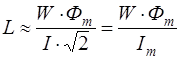. (7.28)

Наконец, с учётом формулы (7.4) получим:

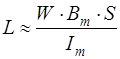. (7.29)

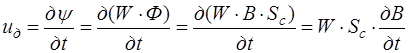, (7.36)

где, S_c – активное сечение магнитопровода;

В – индукция в сердечнике;

W – число витков обмотки дросселя переменного тока.

Из формул (7.34)-(7.36) получим:

Под действием напряжения питания сердечник перемагничивается в положительный полупериод (полярность напряжения питания отмечена на рисунке 12.9 знаками «+», «–») в сторону положительного насыщения, в отрицательный полупериод (полярность отмечена в скобках на рисунке 7.9) – в сторону отрицательного насыщения. При перемагничивании благодаря идеальной кривой намагничивания материала тока в цепи не будет (при реальной кривой намагничивания во время перемагничивания сердечника по обмотке будет протекать небольшой намагничивающий ток i_m, как в трансформаторе при холостом ходу). Так как i_р=0, напряжение питания полностью уравновешивается противо-ЭДС на обмотке дросселя и из (7.37) получим:

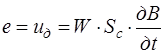. (7.39)

При синусоидальном напряжении питания

e=Е_m·sinwt, (7.40)

w=2·p·f, (7.41)

тогда из (7.39)-(7.41) получим:

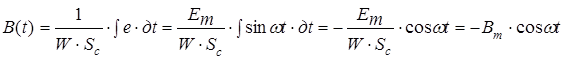, (7.42)

где B_m- амплитудное значение магнитной индукции:

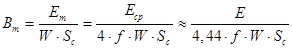(7.43)

Е_m – амплитудное значение напряжения питания;

Е_ср – среднее значение напряжения питания;

Е – действующее значение напряжения питания.