Схема потока жидкости
Из выражения следует, что средние скорости v1 и v2 обратно пропорциональны соответствующим площадям живых сечений S1 и S2 потока жидкости:
v1/v2= S2/S1.
Итак, уравнение неразрывности выражает постоянство объемного расхода Q, а следовательно, и условие неразрывности струи жидкости, по длине установившегося потока жидкости.
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг гидравлических задач.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β.
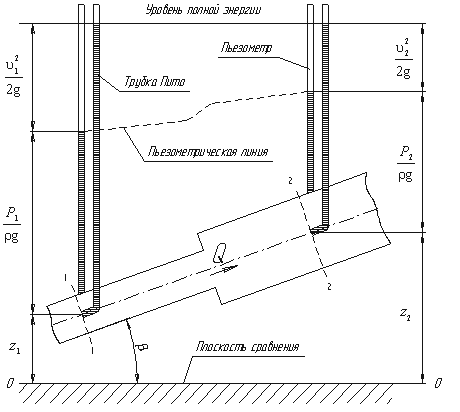
Рисунок – Схема к выводу уравнения Бернулли для идеальной жидкости
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Для измерения давления жидкости применяют пьезометры – тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 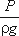 . В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию.
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
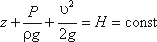
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
z1 и z2 – удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
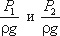 – удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
– удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
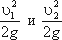 – удельные кинетические энергии в тех же сечениях.
– удельные кинетические энергии в тех же сечениях.
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
Уравнение Бернулли можно истолковать и геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рисунок, можно заметить, что z1 и z2 – геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; 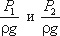 - пьезометрические высоты;
- пьезометрические высоты; 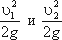 - скоростные высоты в указанных сечениях.
- скоростные высоты в указанных сечениях.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
 Разветвлённые трубопроводы отличаются тем, что они имеют одну общую точку, из которой расходятся разные потоки, или общую точку, в которой несколько разных потоков сходится. Этот вариант наиболее часто встречается в гидросистемах технологического оборудования, где от одной насосной станции питается сразу несколько одновременно работающих потребителей. Для разветвлённых трубопроводов, так же как и для параллельных, можно записать уравнение расходов
Разветвлённые трубопроводы отличаются тем, что они имеют одну общую точку, из которой расходятся разные потоки, или общую точку, в которой несколько разных потоков сходится. Этот вариант наиболее часто встречается в гидросистемах технологического оборудования, где от одной насосной станции питается сразу несколько одновременно работающих потребителей. Для разветвлённых трубопроводов, так же как и для параллельных, можно записать уравнение расходов
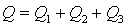 ,
,
где  – расходы в соответствующих ветвях.
– расходы в соответствующих ветвях.
Составим также уравнение Бернулли для любой из ветвей. Будем считать: давление в трубопроводе таково, что нивелирной высотой можно пренебречь. Примем также, что давление в конце каждой ветви (в сечении к), необходимое для преодоления нагрузки, равно  .
.
Уравнение Бернулли для сечений к будет выглядеть следующим образом:
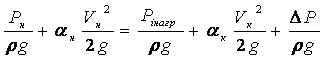 ,
,
где i – индекс, соответствующий определённой ветви.
Если считать, что рассматриваемая система трубопроводов принадлежит гидросистеме технологической машины, в которой давления в различных ветвях, как правило, составляют несколько мегапаскалей, а скорости течения жидкости по трубам чаще всего невысокие (до5 м/c), скоростным напором можно пренебречь. В самом деле, например, при скорости 1 м/c и коэффициенте кинетической энергии ± равен 2, величина скоростного напора составит 0,1 м, что при переводе в единицы давления равно 0,001МПа. С учетом этого и после обычных преобразований получим

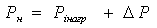 .
.
 Величина
Величина 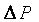 , в данном случае, представляет собой характеристику простого трубопровода и равна
, в данном случае, представляет собой характеристику простого трубопровода и равна 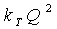 . Таким образом, для каждой ветви разветвлённого трубопровода можно написать подобное уравнение. Если добавить к ним уравнение расходов, то можно получить систему уравнений вида
. Таким образом, для каждой ветви разветвлённого трубопровода можно написать подобное уравнение. Если добавить к ним уравнение расходов, то можно получить систему уравнений вида
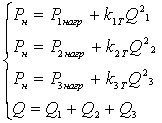 .
.
Подобную систему уравнений можно записать для любого числа ветвей разветвлённого трубопровода. Решая её, можно определить, какой расход и какое давление должен обеспечивать источник гидравлической энергии, чтобы на выходе трубопроводов получалось заданное давление при заданном расходе.
Дата добавления: 2015-06-01; просмотров: 996;
