Тема 7. Течение вязкой жидкости

Вязкость (внутреннее трение) – это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой.

При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Силы внутреннего трения направлены вдоль соприкасающихся слоев и зависят от их относительных скоростей.

Ньютоном была установлена зависимость силы внутреннего трения от сопровождающих его явлений:

F = h|Dv/Dx|s,

где Dv/Dx – градиент скорости (Dx – расстояние между двумя соседними слоями, Dv – разность скоростей жидкости в двух соседних слоях), s – площадь соприкосновения двух соседних слоев, h – коэффициент вязкости, зависящий от природы жидкости и температуры (единица вязкости – паскаль-секунда [Па.с]: 1 Па.с равен вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем 1м/с, возникает сила внутреннего трения 1 Н на 1 м² поверхности касания слоев (1 Па.с = 1 Н.с/м²).

h – коэффициент динамической вязкости;

Ламинарное (слоистое) течение жидкости – когда вдоль потока каждый выделенный слой скользит относительно соседних, не перемешиваясь с ними.

Этот режим наблюдается при небольших скоростях движения жидкости: внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным, а скорости последующих слоев тем больше, чем больше их расстояние до поверхности трубы и наибольшей скоростью обладает слой, движущийся вдоль оси трубы.

Турбулентное (вихревое) течение жидкости – когда вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости.

При этом режиме течения частицы жидкости приобретают составляющие скоростей, перпендикулярные течению и поэтому они могут переходить из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверхности трубы, затем изменяется незначительно. Так как частицы жидкости переходят из одного слоя в другой, то их скорости в различных слоях мало отличаются. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.

Характер течения зависит от безразмерной величины – числа Рейнольдеса

Re = <v>l/ h,

Где h - плотность жидкости, <v> - средняя по сечению трубы скорость жидкости, l- перемещение жидкости по оси x.

При Re < 1000 наблюдается ламинарное течение, в области 1000<Re<2000 происходит переход к турбулентном течению, а при Re > 2300 для гладких труб наблюдается турбулентное течение.

Если число Рейнольдса одинаково, то режим течения различных жидкостей в трубах различных сечений одинаков.

При движении тела в жидкости или газе с небольшими скоростями и малых Re сопротивление среды определяется силами трения и согласно Стоксу, эта сила пропорциональна произведению динамической вязкости на линейные размеры тела и скорости движения тела в жидкости.

Если форма тела – шар, то сила сопротивления при движении падения шара в жидкости, то на него действуют: сила тяжести, выталкивающая сила и сила сопротивления в сторону противоположную движению. Когда силы выравниваются, то движение будет равномерным F1 и F2 - постоянны; F3 зависит от скорости.

ПУАЗЁЙЛЯ ЗАКОН (Хагена - Пуазёйля закон) – закон установившегося течения вязкой несжимаемой жидкости в тонкой цилиндрической трубке круглого сечения.

Сформулирован впервые Г. Хагеном (G. Hagen) в 1839 и вскоре повторно выведен Ж. Л. Пуазёйлем (3. L. Poiseuille) в 1840-41.

Согласно закону Пуазейля, секундный объёмный расход жидкости пропорционален перепаду давления на единицу длины трубки:

где Q – объём жидкости, протекающей за 1 с через сечение трубки,

r и p₀ – давление в двух сечениях трубки,

d – диаметр трубки,

l – расстояние между сечениями,

m – коэф. вязкости.

Связь коэф. k с коэф. вязкости m установлена в 1845 Дж. Стоксом (G. Stokes):

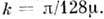
Закон Пуазейля применим только при ламинарном течении жидкости и при условии, что длина трубки превышает т. н. длину нач. участка, необходимую для развития ламинарного течения в трубке. Течение, подчиняющееся закону Пуазейля, наз. течением Пуазёйля; оно характеризуется параболическим распределением скорости по радиусу трубки д_:

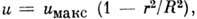
где и – скорость на расстоянии r от оси,

u_макс – скорость на оси трубки.

В ламинарном течении, подчиняющемся закону Пуазейля, в каждом поперечном сечении трубки ср. скорость 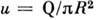вдвое меньше макс. скорости u_макс в этом сечении.

Закон Пуазейля применяется для определения коэффициента вязкости разложения жидкостей при различных температурах посредством капиллярных вискозиметров