Вычитание векторов.
Определение 5. Разностью векторов 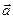 и
и 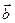 называется такой вектор
называется такой вектор 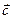 что сумма
что сумма 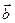 и
и 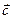 равна
равна 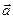 , т.е если
, т.е если 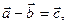 то
то 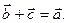
Чтобы из одного вектора вычесть другой, нужно отнести их к общему началу и провести вектор из конца вектора – вычитаемого в конец вектора уменьшаемого. Так 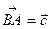 - разность
- разность 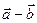

Умножение вектора на число.
Определение 6. Произведением вектора на 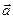 число
число 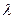 называется вектор, имеющий направление вектора
называется вектор, имеющий направление вектора 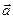 , если
, если 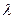 >0, и противоположное направление, если
>0, и противоположное направление, если 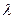 <0. Длина этого вектора равна произведению длины вектора
<0. Длина этого вектора равна произведению длины вектора 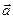 на модуль числа
на модуль числа 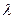 .
.
Если 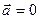 , то
, то 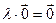 для любых
для любых 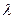 .
.
Если 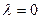 , то
, то 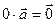 для любого
для любого 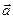

§3.3 Разложение вектора по базису. Координаты вектора.
Определение 7. Назовем базисом в пространстве три некомпланарных вектора, взятых в определенном порядке.
Базис 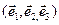 позволяет однозначно сопоставить каждому вектору упорядоченную тройку чисел
позволяет однозначно сопоставить каждому вектору упорядоченную тройку чисел 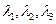 - коэффициенты разложения этого вектора по векторам базиса. Наоборот, каждой упорядоченной тройке чисел
- коэффициенты разложения этого вектора по векторам базиса. Наоборот, каждой упорядоченной тройке чисел 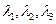 при помощи базиса мы сопоставим вектор, если составим линейную комбинацию
при помощи базиса мы сопоставим вектор, если составим линейную комбинацию 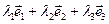 .
.
Определение 8. Если 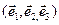 - базис и
- базис и 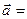
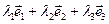 , то числа
, то числа 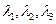 называются координатами вектора в данном базисе. Принята запись
называются координатами вектора в данном базисе. Принята запись 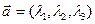 .
.
Аналогично определяются координаты вектора на плоскости.
Определение 9. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка – начало координат; прямые, проходящие через начало координат в направлении базисных векторов – осями координат. Первая – осью абсцисс, вторая – осью ординат, третья – осью аппликат.
Плоскости, проходящие через оси координат, называются координатными плоскостями. Координаты радиуса – вектора точки М, назовем координатами самой точки М, М(х;y;z).
В декартовой системе координат базис 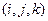 назовем ортонормированным. Его векторы попарно ортогональны и по длине равны единице. Все они имеют общее начало точку О(0;0;0) и направление соответственно осям координат. Будем называть их единичными или ортами. Тогда любой вектор
назовем ортонормированным. Его векторы попарно ортогональны и по длине равны единице. Все они имеют общее начало точку О(0;0;0) и направление соответственно осям координат. Будем называть их единичными или ортами. Тогда любой вектор 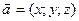 можно разложить по ортам, записав его в виде комбинации
можно разложить по ортам, записав его в виде комбинации 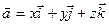 , где
, где 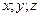 - координаты вектора.
- координаты вектора. 
 §3.4 Линейные операции над векторами, заданными своими координатами.
§3.4 Линейные операции над векторами, заданными своими координатами.
Пусть в базисе 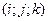 заданы векторы
заданы векторы 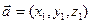 и
и 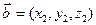
1. Сложение. Каждая координата суммы двух (или более) векторов равна сумме соответствующих координат слагаемых:
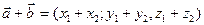
2. Вычитание. 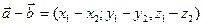
Пусть в декартовой системе координат вектор задан двумя точками
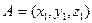 и
и 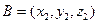 Найти координаты вектора
Найти координаты вектора 
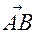
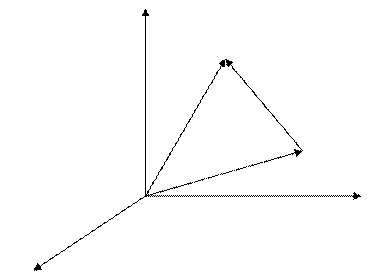 По правилу вычитания векторов
По правилу вычитания векторов 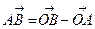 Согласно определению координат точки:
Согласно определению координат точки: 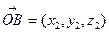
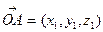
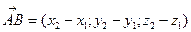
Чтобы найти координаты вектора, заданного координатами точек начала и конца, надо из координат конца вектора вычесть соответствующие координаты начала.
Пример. А(-1;2;3) В(0;-1;1)
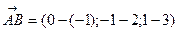 =(1;-3;-2);
=(1;-3;-2); 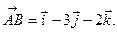
3. Умножение вектора на число.
Каждая координата произведения вектора на число равна произведению соответствующей координаты данного вектора на это число: 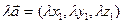
4. Деление отрезка в данном отношении
Задача. Даны точки 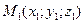 и
и 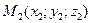 Найти точку
Найти точку 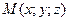 , делящую отрезок М1М2 в отношении
, делящую отрезок М1М2 в отношении 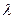
 |
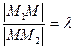
Решение:
Найдем координаты векторов 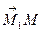 и
и 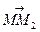
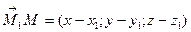
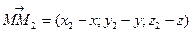
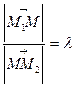 тогда
тогда
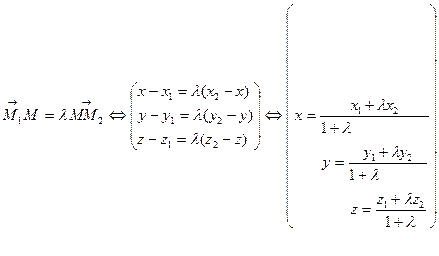 -координаты М, делящей отрезок в отношении
-координаты М, делящей отрезок в отношении 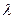
Положив 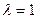 Найдем координаты середины отрезка.
Найдем координаты середины отрезка.
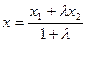
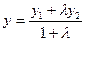
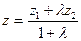
Пример. А(-2;1), В(3;6) Разделить отрезок в отношении 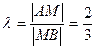
Ответ: М(0;3)
5. Условие коллинеарности векторов.
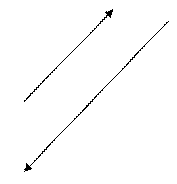 Если векторы
Если векторы 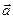 и
и 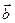 коллинеарны, то всегда можно найти такое число
коллинеарны, то всегда можно найти такое число 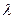 , что
, что 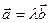 . В координатах это условие выглядит так:
. В координатах это условие выглядит так: 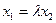 ,
, 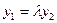 ,
, 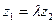 ,
, 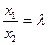 ,
, 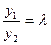 ,
, 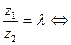 или
или 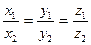 -условие коллинеарности двух векторов.
-условие коллинеарности двух векторов.
Пример. При каком значении р векторы 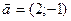 ,
, 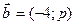 будут коллинеарны.
будут коллинеарны.
Ответ: - 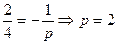
Дата добавления: 2015-05-30; просмотров: 1742;
