Колебательный контур
Колебательный контур является основой линейной части лампового генератора. Простейшие колебательные контуры состоят из параллельного соединения индуктивности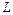 
и емкости 
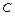(рис.44.4,а) или из их последовательного соединения (рис.44.4,б).
Если колебательный контур не содержит активных сопротивлений, он называется идеальным.
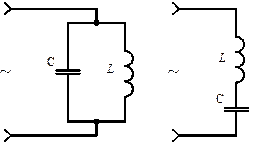
а б
Рис.44.4. Основные типы колебательных контуров (LC)
Собственная частота колебательного контура
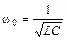. (44.1)
Величину ω0 называют резонансной частотой контура. Обычно в большинстве ламповых генераторов собственная частота колебаний ω0 и частота, на которой работает генератор, равны.
При резонансной частоте индуктивное и емкостное сопротивления равны между собой:
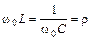, (44.2)
где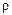 
– волновое или характеристическое сопротивление колебательного контура.
С учетом выражения (44.1) волновое сопротивление можно выразить через параметры контура
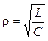. (44.3)
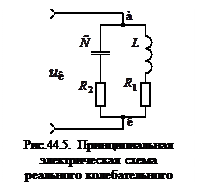
Если ветви колебательного контура содержат активные сопротивления, такой контур называется реальным. Принципиальная электрическая схема реального колебательного контура приведена на рис.44.5.
Если ламповый генератор служит источником питания установки индукционного нагрева, то основное активное сопротивление сосредоточено в ветви с индуктивностью и R1 >> R2. В этом случае величиной R2 можно пренебречь.
Если ламповый генератор служит источником питания установки диэлектрического нагрева, то основное активное сопротивление сосредоточено в ветви с емкостью и R2 >> R1. Сопротивлением R1 можно пренебречь.
Комплексное электрическое сопротивление реального колебательного контура
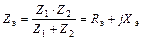, (44.4)
где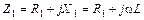 
– комплексное электрическое сопротивление ветви с индуктивностью; 
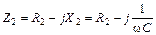– комплексное индуктивное сопротивление ветви с емкостью; 
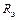– эквивалентное активное сопротивление колебательного контура; 
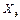– эквивалентное реактивное сопротивление.
Выражение для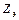 
можно представить в следующем виде:
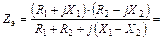
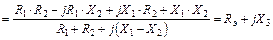(44.5)
Собственная (резонансная) частота реального колебательного контура
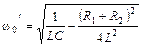. (44.6)
Отношение реактивной мощности контура к активной называется его добротностью и обозначается буквой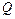 
. Для обеспечения высокой добротности параметры колебательного контура должны быть такими, что 
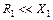и 
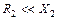. При резонансе токов в параллельном контуре 
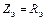и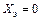 
. Если принять, что в режиме резонанса токов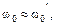 
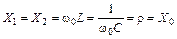и с учетом соотношени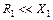й и 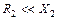получим приближенную формулу для расчета величины Rэ
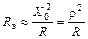или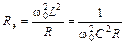 
, (44.7)
где R = R1 + R2.
Добротность колебательного контура в этом случае можно рассчитать по формуле
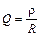(44.8)
Дата добавления: 2015-05-30; просмотров: 1433;