Обработка результатов измерений и оценка их точности
Никакие измерения не могут быть выполнены абсолютно точно, полученный результат всегда содержит некоторую погрешность. Различают систематические, случайные и грубые погрешности. Систематическими называют погрешности, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины (следствие работы с неисправными приборами, применение неточных методов измерений, другие упущения исследователя). Такие погрешности чаще всего характеризуются постоянством знака, т.е. уменьшают или увеличивают результат. Дляисключения систематических погрешностей пользуются следующими правилами. При проведении эксперимента необходимо использовать только средства измерения, прошедшие метрологический контроль (проверку). Желательно также, чтобы измерения одной и той же величины дублировались применением различных средств измерений. При длительных экспериментальных исследованиях необходима контрольная тарировка измерительных средств. При определении величин по результатам косвенных измерений целесообразно изменить метод их вычисления.
Случайными называют погрешности, которые при повторных измерениях одной и той же величины изменяются случайным образом. Они вызываются различными объективными и субъективными причинами.
При многократных определениях какой-либо величины для однихи тех же условий могут встречаться результаты, которые значительно отличаются от других той же серии, т.е. грубые погрешности. Они зачастую вызваны невнимательностью экспериментатора и должны быть обязательно исключены. Известны различные методы исключения грубых погрешностей. Грубые погрешности по критерию максимального отклонения исключают следующим образом. По полученным опытным данным находят среднее арифметическое значение величины и ее среднеквадратичное отклонение. Для сомнительного результата  находят относительное отклонение
находят относительное отклонение
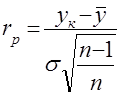 ,
,
где –число опытов.
–число опытов.

Рис. 9. Методы определения средней величины по записи прибора: а – планиметрирования; б – ординат; в – классных промежутков

Рис. 10. Схема грунтового канала
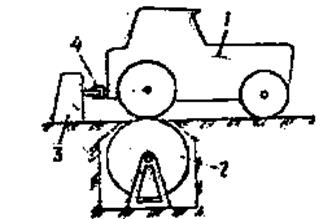
Рис. 11. Схема стенда с беговыми барабанами для тяговых испытаний
Если абсолютное значение величины 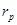 превышает табличное значение
превышает табличное значение  то данный результат является грубой ошибкой и его необходимо при последующей обработке опытных данных исключить.
то данный результат является грубой ошибкой и его необходимо при последующей обработке опытных данных исключить.
Грубые погрешности могут быть определены в по критерию Стьюдента. Значение этого критерия для сомнительного результата вычисляют
по соотношению
 .
.
Если полученное значение  по абсолютной величине больше табличного
по абсолютной величине больше табличного  , данный результат из последующей обработки должен быть исключен.
, данный результат из последующей обработки должен быть исключен.
Перед подбором эмпирических формул по данным опытов следует убедиться в достоверности последних, т.е. вих воспроизводимости с заданной доверительной вероятностью. Оценка воспроизводимости опытных данных осуществляется по критерию Кохрена:
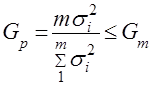 ,
,
где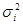 –наибольшее значение дисперсиииз числа
–наибольшее значение дисперсиииз числа 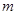 параллельно поставленныхсерий опытов;
параллельно поставленныхсерий опытов; 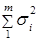 – сумма дисперсий
– сумма дисперсий  серий опытов
серий опытов 
Если полученное число  меньше табличного
меньше табличного ,опыты считают воспроизводимыми.
,опыты считают воспроизводимыми.
При исследовании процессов, связанных с производственной и технической эксплуатацией машин, обеспечением их надежности, часто наблюдают случайные величины, изменяющиеся в каком-то интервале с различной плотностью. Обработку таких наблюдений осуществляют методами математической статистики.
Пусть для различных значений величины имеем большое число наблюдений величины
имеем большое число наблюдений величины  . Тогда диапазон изменения величины
. Тогда диапазон изменения величины  разбивают на
разбивают на 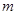 равных интервалов
равных интервалов  и подсчитывают, сколько раз наблюдаемая величина
и подсчитывают, сколько раз наблюдаемая величина  попадает в каждый интервал; очевидно, что
попадает в каждый интервал; очевидно, что  , где
, где  – число наблюдений. Относя наблюдаемое для каждого интервала изменения
– число наблюдений. Относя наблюдаемое для каждого интервала изменения  количество наблюдаемых величин
количество наблюдаемых величин  к общему числу наблюдений, строят гистограмму (рис. 12). Эти экспериментальные данные можно аппроксимировать теоретической кривой – нормальным законом, законами Пуассона, Вейбула, биномиальным, логарифмическим и др. Соответствие выбранной теоретической кривой опытным данным проверяют по различным критериям. При больших количествах статистическихизмерений часто применяют критерий Пирсона. Критерий согласия Пирсона.
к общему числу наблюдений, строят гистограмму (рис. 12). Эти экспериментальные данные можно аппроксимировать теоретической кривой – нормальным законом, законами Пуассона, Вейбула, биномиальным, логарифмическим и др. Соответствие выбранной теоретической кривой опытным данным проверяют по различным критериям. При больших количествах статистическихизмерений часто применяют критерий Пирсона. Критерий согласия Пирсона.
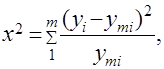
где  – число наблюдений величины
– число наблюдений величины  в
в  -м интервале;
-м интервале; 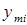 – число наблюдений величины
– число наблюдений величины  , определяемое выбранным теоретическим законом.
, определяемое выбранным теоретическим законом.
При соответствии теоретической кривой опытным данным должно выполняться условие
 ,
,
где  – уровень значимости, обычно принимаемый 0,01.
– уровень значимости, обычно принимаемый 0,01.
Значение критерия Пирсона  определяют по таблице.
определяют по таблице.

Рис. 12. Гистограмма и кривая распределения случайных величин
Адекватность теоретических зависимостей опытным данным может быть установлена по критерию Фишера. По данным аналитического исследования строят графические зависимости характеристик изучаемого процесса от влияющих факторов и здесь же наносят точки либо кривые, полученные в ходе эксперимента. Естественно, что полное совпадение расчетных и опытных данных будет лишь в отдельных местах, отклонения же между опытными и расчетными результатами характеризуют точность последних. Такое отклонение характеризуют относительной погрешностью, т.е. отношением разности между опытным и расчетным значениями величины к опытной величине, выраженными в процентах. Обычно указывают минимальную и максимальную погрешности. Либо их предельное значение. Поскольку опытное значение величины также получено с определенной точностью, отклонение расчетных данных может лежать либо в пределах погрешности эксперимента, либо выходить за них. Последнее, по сути, и характеризует приемлемость принятых в аналитических исследованиях допущений.
В зависимости от целей проводимого исследования задаются допустимой точностью расчетных результатов. При расчетах, связанных с определением прочности конструкций машин, приемлемой считается точность 5...I0%, при проведении исследований рабочих процессов машин – до I5...20%, что обусловлено изменчивостью свойств, разрабатываемых сред. Располагая значением допустимой погрешности расчетных результатов, по построенным графическим зависимостям определяют диапазон изменения факторов, характеризующий область применения аналитических зависимостей. Если такой диапазон изменения факторов соответствует задачам исследования, то делают заключение об удовлетворительном соответствии расчетных и опытных данных. В противном случае необходима корректировка аналитической модели, переоценкой приемлемости принятых допущений, что может составить предмет самостоятельного исследования.
На основе анализа расчетных и опытных данных формулируют основные выводы и результаты проведенного исследования, определяют направление дальнейших исследований. Выводы должны отражать физическую сущность познанных закономерностей, степень влияния на характеристики процесса различных факторов, возможности количественной оценки характеристик процесса с необходимой точностью. В результатах исследования отражают возможности использования основных положений теоретических разработок, построенной методики проведения эксперимента, степень соответствия расчетных и опытных данных, формулируют также целесообразные дальнейшие направления как теоретических, так и экспериментальных исследований.
Дата добавления: 2015-05-30; просмотров: 1577;
