Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 16 страница

Из выражений (220.4) и (220.6) следует, что

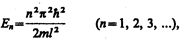(220.7)

т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потен­циальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е_n, зависящих от целого числа п. Следовательно, энергия Е_n частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения,т.е.квантуется. Квантованные значения энергии Е_n называютсяуровнями энергии, а число п, определяющее энергетические уровни частицы, называетсяглавным квантовым числом. Таким образом, микрочастица в «по­тенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Е_n, или, как говорят, частица находится в кван­товом состоянии n.

Подставив в (220.5) значение k из (220.6), найдем собственные функции:

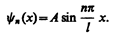
Постоянную интегрирования А найдем из условия нормировки (216.3), которое для данного случая запишется в виде

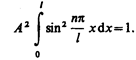
В результате интегрирования получим А = 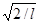, а собственные функции будут иметь вид

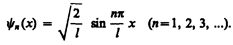(220.8)

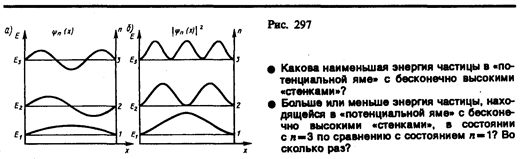
Графики собственных функций (220.8), соответствующие уровням энергии (220.7) при n = 1, 2, 3, приведены на рис. 297,а. На рис. 297,6 изображена плотность вероят­ности обнаружения частицы на различных расстояниях от «стенок» ямы, равная |y_n(х)|² = y_n(х)y*_n(х) для n=1,2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n=2 частица не может находиться в середине «ямы», в то времякакодинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.

Из выражения (220.7) вытекает, что энергетический интервал между двумя сосед­ними уровнями равен

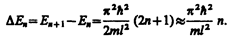(220.9)

Например, для электрона при размерах ямы l=10^–1 м (свободные электроны в метал­ле) DE_n » 10^–35n Дж » 10^–16n эВ, т. е. энергетические уровни расположены столь тесно, что спектр практически можно считать непрерывным. Если же размеры ямы соизмеримы с атомными (l»10^–10 м), то для электрона DE_n » 10^–17n Дж » 10²n эВ, т. е. получаются явно дискретные значения энергии (линейчатый спектр). Таким об­разом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконеч­но высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не накладывает.

Кроме того, квантово-механическое рассмотрение данной задачи приводит к выво­ду, что частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная . Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты Dх частицы в «яме» шириной l рав­на Dx=l. Тогда, согласно соотношению неопределенностей (215.1), импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса Dp»h/l. Такому разбросу значений импульса соответствует кинетическая энергия E_min»(Dp)²/(2m) = h²/(2ml²). Все остальные уровни (n>1) имеют энергию, превыша­ющую это минимальное значение.

Из формул (220.9) и (220.7) следует, что при больших квантовых числах (n>>1) DE_n/E_n»2/n<<1, т. е. соседние уровни расположены тесно: тем теснее, чем больше n. Если n очень велико, то можно говорить о практически непрерывной последователь­ности уровней и характерная особенность квантовых процессов — дискретность — сглаживается. Этот результат является частным случаем принципа соответствия Бора (1923), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.

Более общая трактовка принципа соответствия, имеющего огромную роль в со­временной физике, заключается в следующем: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применения, причем в определенных пре­дельных случаях новая теория переходит в старую. Так, формулы кинематики и дина­мики специальной теории относительности переходят при v<<с в формулы механики Ньютона. Например, хотя гипотеза де Бройля приписывает волновые свойства всем телам, но в тех случаях, когда мы имеем дело с макроскопическими телами, их волновыми свойствами можно пренебречь, т. е. применять классическую механику Ньютона.

§ 221. Прохождение частицы сквозь потенциальный барьер. Туннельный эффект

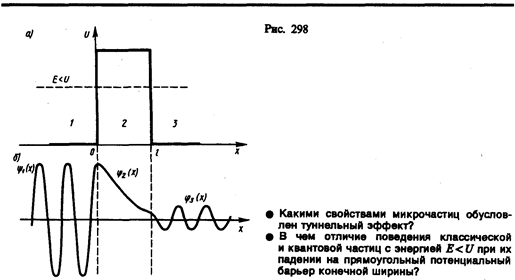
Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 298, а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямо­угольной формы высоты U и ширины lможем записать

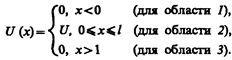
При данных условиях задачи классическая частица, обладая энергией Е, либо бес­препятственно пройдет над барьером (при Е>U), либо отразится от него (при Е<U) и будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при Е>U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E<U имеется также отличная от нуля вероятность, что частица окажется в области х>1, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, описывающего движение микро­частицы при условиях данной задачи.

Уравнение Шредингера (217.5) для стационарных состояний для каждой из выде­ленных на рис. 298, а области имеет вид

(221.1)

Общие решения этих дифференциальных уравнений:

(221.2)

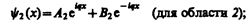
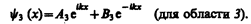(221.3)

В частности, для области 1 полная волновая функция, согласно (217.4), будет иметь вид

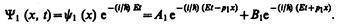(221.4)

В этом выражении первый член представляет собой плоскую волну типа (219.3), распространяющуюся в положительном направлении оси х (соответствует частице, движущейся в сторону барьера), а второй — волну, распространяющуюся в проти­воположном направлении, т. е. отраженную от барьера (соответствует частице, движу­щейся от барьера налево).

Решение (221.3) содержит также волны (после умножения на временной множи­тель), распространяющиеся в обе стороны. Однако в области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффици­ент B₃ в формуле (221.3) следует принять равным нулю.

В области 2 решение зависит от соотношений Е>U или Е<U. Физический интерес представляет случай, когда полная энергия частицы меньше высоты потенциального барьера, поскольку при Е<U законы классической физика однозначно не разрешают частице проникнуть сквозь барьер. В данном случае, согласно (221.1), q=ib — мнимое число, где

Учитывая значение q и B₃=0, получим решения уравнения Шредингера для трех областей в следующем виде:

(221.5)

В области 2 функция (221.5) уже не соответствует плоским волнам, распространя­ющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а дейст­вительные. Можно показать, что для частного случая высокого и широкого барьера, когда bl >>1, B₂»0.

Качественный характер функций y₁(х), y₂(х) и y₃(x) иллюстрируется на рис. 298, б, откуда следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. Следовательно, получили, что частица имеет отличную от нудя вероятность прохождения сквозь потенциальный барьер конечной ширины.

Таким образом, квантовая механика приводит к принципиально новому специфи­ческому квантовому явлению, получившему название туннельного эффекта, в резуль­тате которого микрообъект может «пройти» сквозь потенциальный барьер.

Для описания туннельного эффекта используют понятиекоэффициента прозрач­ности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих. Можно показать, что

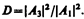
Для того чтобы найти отношение |А₃/А₁|², необходимо воспользоваться условиями непрерывности y и y' на границах барьера х=0 и х=l (рис. 298):

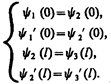(221.6)

Эти четыре условия дают возможность выразить коэффициенты A₂, A₃, В₁ и В₂ через А₁. Совместное решение уравнений (221.6) для прямоугольного потенциального барьера дает (в предположении, что коэффициент прозрачности мал по сравнению с единицей)

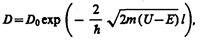(221.7)

где U — высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D₀ — постоянный множитель, который можно приравнять единице. Из выражения (221.7) следует, что D сильно зависит от массы т частицы, ширины l барьера и от (U—E); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.

Для потенциального барьера произвольной формы (рис. 299), удовлетворяющей условиям так называемого квазиклассического приближения (достаточно гладкая форма кривой), имеем

где U=U(x).

С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е<U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специ­фическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса Dр на отрезке Dх=l составляет Dp>h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия (Dр)²/(2m) может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной.

Основы теории туннельных переходов заложены работами Л. И. Мандельштама и М. А. Леонтовича (1903—1981). Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций).

§ 222. Линейный гармонический осциллятор в квантовой механике

Линейный гармонический осциллятор — система, совершающая одномерное движение под действием квазиупругой силы, — является моделью, используемой во многих задачах классической и квантовой теории (см. § 142). Пружинный, физический и мате­матический маятники — примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора (см. (141.5)) равна

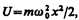(222.1)

где w₀ — собственная частота колебаний осциллятора, т — масса частицы. Зависи­мость (222.1) имеет вид параболы (рис. 300), т. е. «потенциальная яма» в данном случае является параболической.

Амплитуда малых колебаний классического осциллятора определяется его полной энергией Е (см. рис. 16). В точках с координатами ±x_max полная энергия Е равна потенциальной энергии. Поэтому с классической точки зрения частица не может выйти за пределы области (–x_max, +x_max). Такой выход означал бы, что ее потенциальная энергия больше полной, что абсурдно, так как приводит к выводу, что кинетическая энергия отрицательна. Таким образом, классический осциллятор находится в «потенци­альной яме» с координатами – x_max <х< x_max «без права выхода» из нее.

Гармонический осциллятор в квантовой механике —квантовый осциллятор — опи­сывается уравнением Шредингера (217.5), учитывающим выражение (222.1) для потен­циальной энергии. Тогда стационарные состояния квантового осциллятора определя­ются уравнением Шредингера вида

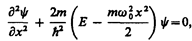(222.2)

где Е — полная энергия осциллятора. В теории дифференциальных уравнений до­казывается, что уравнение (222.2) решается только при собственных значениях энергии

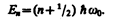(222.3)

Формула (222.3) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т. е. квантуется. Энергия ограничена снизу отличным от нуля, как и для прямоугольной «ямы» с бесконечно высокими «стенками» (см. § 220), минималь­ным значением энергии E₀=¹/₂ћw₀^. Существование минимальной энергии — она назы­вается энергией нулевых колебаний — является типичной для квантовых систем и пред­ставляет собой прямое следствие соотношения неопределенностей.

Наличие нулевых колебаний означает, что частица не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. В самом деле, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда неопределенность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в «потенциальной яме».

Вывод о наличии энергии нулевых колебаний квантового осциллятора противоре­чит выводам классической теории, согласно которой наименьшая энергия, которую может иметь осциллятор, равна нулю (соответствует покоящейся в положении равно­весия частице). Например, классическая физика приводит к выводу, что при Т=0 энергия колебательного движения атомов кристалла должна обращаться в нуль. Следовательно, должно исчезать и рассеяние света, обусловленное колебаниями атомов. Однако эксперимент показывает, что интенсивность рассеяния света при понижении температуры не равна нулю, а стремится к некоторому предельному значению, указывающему на то, что при Т®0 колебания атомов в кристалле не прекращаются. Это является подтверждением наличия нулевых колебаний.

Из формулы (222.3) также следует, что уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга (рис. 300), а имен­но расстояние между соседними энергетическими уровнями равно ћw₀, причем мини­мальное значение энергии E₀=¹/₂ћw₀.

Строгое решение задачи о квантовом осцилляторе приводит еще к одному значи­тельному отличию от классического рассмотрения. Квантово-механический расчет показывает, что частицу можно обнаружить за пределами дозволенной области |x|£x_max (см. рис. 16), в то время как с классической точки зрения она не может выйти за пределы области (–x_max, +x_max). Таким образом, имеется отличная от нуля вероят­ность обнаружить частицу в той области, которая является классически запрещенной. Этот результат (без его вывода) демонстрируется на рис. 301, где приводится кван­товая плотность вероятности w обнаружения осциллятора для состояния п=1. Из рисунка следует, что для квантового осциллятора действительно плотность вероятности w имеет конечные значения за пределами классически дозволенной области |x|£x_max, т.е. имеется конечная (но небольшая) вероятность обнаружить частицу в области за пределами «потенциальной ямы». Существование отличных от нуля значений w за пределами «потенциальной ямы» объясняется возможностью прохожде­ния микрочастиц сквозь потенциальный барьер (см. § 221).

Глава 29 Элементы современной физики атомов и молекул

§ 223. Атом водорода в квантовой механике

Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелияНе⁺, двукратно ионизованного лития Li⁺⁺и др.) сводится к задаче о движении электрона в кулоновском поле ядра.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1),

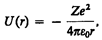(223.1)

где r — расстояние между электроном и ядром. Графически функция U(r) изображена жирной кривой на рис. 302. U(r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает.

Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнению Шредингера (217.5), учитывающему значение (223.1):

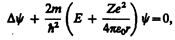(223.2)

где т — масса электрона, Е — полная энергия электрона в атоме. Так как поле, в котором движется электрон, является центрально-симметричным, то для решения уравнения (223.2) обычно используют сферическую систему координат: r, q, j. Не вдаваясь в математическое решение этой задачи, ограничимся рассмотрением важней­ших результатов, которые из него следуют, пояснив их физический смысл.

1. Энергия. В теории дифференциальных уравнений доказывается, что уравнения типа (223.2) имеют решения, удовлетворяющие требованиям однозначности, конеч­ности и непрерывности волновой функции y, только при собственных значениях энергии

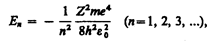(223.3)

т. е. для дискретного набора отрицательных значений энергии.

Таким образом,как и в случае «потенциальной ямы» с бесконечно высокими «стенками» (см. § 220) и гармонического осциллятора (см. § 222), решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения Е₁, E₂, Е₃,... показаны на рис. 302 в виде горизонтальных прямых. Самый нижний уровень Е₁, отвечающий минимальной возможной энер­гии, —основной, все остальные (Е_n >Е₁, n = 2, 3, ...) —возбужденные (см. § 212). При Е<0 движение электрона являетсясвязанным — он находится внутри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n=¥ E_¥ = 0. При Е>0 движение электрона являетсясвободным; область непрерывного спектра Е>0 (заштри­хована на рис. 302) соответствуетионизованному атому. Энергия ионизации атома водорода равна

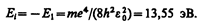
Выражение (223.3) совпадает с формулой (212.3), полученной Бором для энергии атома водорода. Однако если Бору пришлось вводить дополнительные гипотезы (постулаты), то в квантовой механике дискретные значения энергии, являясь следстви­ем самой теории, вытекают непосредственно из решения уравнения Шредингера.

2. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (223.2) удовлетворяют собственные функции 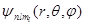, определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным т_l.

Главное квантовое число n, согласно (223.3), определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения начиная с еди­ницы:

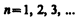
Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой

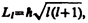(223.4)

где l — орбитальное квантовое число, которое при заданном n принимает значения

(223.5)

т. е. всего n значений, и определяет момент импульса электрона в атоме.

Из решения уравнений Шредингера следует также, что вектор L_l момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L_lx на направление z внешнего магнитного поля принимает квантованные значения, кратные ћ:

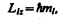(223.6)

где т_l — магнитное квантовое число, которое при заданном l может принимать значения

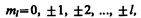(223.7)

т. е. всего 2l+1 значений. Таким образом,магнитное квантовое число m_l определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентации.

Наличие квантового числа m_l должно привести в магнитном поле к расщеплению уровня с главным квантовым числом п на 2l+1 подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий. Действительно, расщеп­ление энергетических уровней в магнитном поле было обнаружено в 1896 г. голландс­ким физиком П. Зееманом (1865—1945) и получило названиеэффекта Зеемана. Расщеп­ление уровней энергии во внешнем электрическом поле, тоже доказанное эксперимен­тально, называетсяэффектом Штарка*.

* И. Штарк (1874—1957) — немецкий физик.

Хотя энергия электрона (223.3) и зависит только от главного квантового числа п, но каждому собственному значению Е_n (кроме Е₁) соответствует несколько собственных функций , отличающихся значениями l и m_l. Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Так как при данном п орбитальное квантовое число l может изменяться от 0 до п–1 (см. (223.5)), а каждому значению l соответствует 2l+1 различных значений m_l (223.7), то число различных состояний, соответствующих данному п, равно

(223.8)

Квантовые числа и их значения являются следствием решений уравнений Шредингера и условий однозначности, непрерывности и конечности, налагаемых на волновую функцию y. Кроме того, так как при движении электрона в атоме существенны волновые свойства электрона, то квантовая механика вообще отказывается от клас­сического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема.

Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в раз­личных точках объема атома. Квантовые числа п и l характеризуют размер и форму электронного облака, а квантовое число m_l характеризует ориентацию электронного облака в пространстве.

В атомной физике, по аналогии со спектроскопией, состояние электрона, харак­теризующееся квантовыми числами l=0, называют s-состоянием (электрон в этом состоянии называют s-электроном), l=1 — p-состоянием, l=2 — d-состоянием, l=3 — f-состоянием и т. д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях n=2 и l=0 и 1 обозначаются соответственно символами 2s и 2р.

На рис. 303 для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при n=1 и п=2, определяемое | |². Как видно из рисунка, оно зависит от n, l и m_l. Так, при l=0 электронная плотность отлична от нуля в центре и не зависит от направления (сферически-симмет­рична), а для остальных состояний в центре равна нулю и зависит от направления.

3. Спектр. Квантовые числа n, l и m_l позволяют более полно описать спектр испускания (поглощения) атома водорода, полученный в теории Бора (см. рис. 294).

В квантовой механике вводятсяправила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света. Те­оретически доказано и экспериментально подтверждено, что для дипольного излучения электрона, движущегося в центрально-симметричном поле ядра, могут осуществляться только такие переходы, для которых: 1) изменение орбитального квантового числа Dl удовлетворяет условию

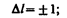(223.9)

2) изменение магнитного квантового числа Dm_l удовлетворяет условию

В оптических спектрах указанные правила отбора в основном выполняются. Одна­ко в принципе могут наблюдаться и слабые «запрещенные» линии, например воз­никающие при переходах с Dl = 2. Появление этих линий объясняется тем, что строгая теория, запрещая дипольные переходы, разрешает переходы, соответствующие излуче­нию более сложных систем зарядов, например квадруполей. Вероятность же квадрупольных переходов (переходы с Dl=2) во много раз меньше вероятности дипольных переходов, поэтому «запрещенные» линии и являются слабыми.

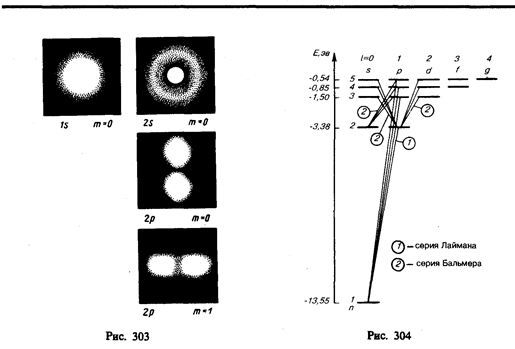
Учитывая число возможных состояний, соответствующих данному n, и правило отбора (223.9), рассмотрим спектральные линии атома водорода (рис. 304): серии Лаймана соответствуют переходы

серии Бальмера —

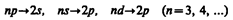
и т. д.