Концентрация зарядов в полупроводнике

Равновесная концентрация зарядов в собственном полупроводнике

Вероятность s(W) нахождения свободного электрона в энергетическом состоянии W определяется статистической функцией Ферми — Дирака:

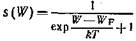
где W_F – уровень энергии, которой электрон может обладать с вероятностью s = l/2 (уровень Ферми); в собственном полупроводнике он находится примерно посередине запрещенной зоны: W_F ~ (W_c + Wv)/2;
kT – средняя энергия теплового движения микрочастицы при температуре
Т К;
k=1,38 10^–23 Дж/К — постоянная Больцмана.

Число дырок в идеальной кристаллической решетке собственного полупроводника равно числу свободных электронов:

p_i = n_i

Величины концентраций электронов и дырок представляют собой результат динамического равновесия двух процессов – генерации и рекомбинации подвижных носителей заряда.

Скорость рекомбинации, т. е. число исчезающих в единицу времени электронно–дырочных пар, определяется свойствами полупроводника; кроме того, она пропорциональна концентрации электронов и дырок, так как чем больше число носителей заряда, тем вероятнее их встреча, завершающаяся рекомбинацией. Таким образом, скорость рекомбинации

v_рек= γ_in_ip_i= γ·n²_i,

где γ_i– коэффициент рекомбинации, определяемый свойствами полупроводника.

Скорость генерации – число освобождающихся в единицу времени электронно–дырочных пар – зависит от температуры полупроводника и ширины его запрещенной зоны.

В стационарном режиме должно существовать динамическое равновесие – скорость генерации должна равняться скорости рекомбинации:

v_ген= γ·n²_i

Отсюда n²_i = v_ген /γ .