Распределение скоростей молекул по Максвеллу. Измерение скоростей молекул. Опыт Штерна. Опытная проверка распределения молекул по скоростям.
В результате многочисленных соударений молекул газа между собой (~109 столкновений за 1 секунду) и со стенками сосуда, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равновероятными, а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям.
При столкновениях скорости молекул изменяются случайным образом. Может оказаться, что одна из молекул в ряде столкновений будет получать энергию от других молекул и ее энергия будет значительно больше среднего значения энергии при данной температуре. Скорость такой молекулы будет большая, но, все-таки она будет иметь конечное значение, так как максимально возможная скорость – скорость света - 3·108 м/с. Следовательно, скорость молекулы вообще может иметь значения от 0 до некоторой υmax. Можно утверждать, что очень большие скорости по сравнению со средними значениями, встречаются редко, также как и очень малые.
Как показывают теория и опыты распределение молекул по скоростям не случайное, а вполне определенное. Определим сколько молекул, или какая часть молекул обладает скоростями, лежащими в некотором интервале вблизи заданной скорости.
Пусть в данной массе газа содержится N молекул, при этом dN молекул обладают скоростями, заключенными в интервале от υ до υ+dυ. Очевидно, что это число молекул dN пропорционально общему числу молекул N и величине заданного интервала скорости dυ
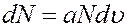 (1)
(1)
где a - коэффициент пропорциональности.
Также очевидно, что dN зависит и от величины скорости υ, так как в одинаковых по величине интервалах, но при разных абсолютных значениях скорости число молекул будет различным (пример: сравните число живущих в возрасте 20 – 21 год и 99 – 100 лет). Это значит, что коэффициент a в формуле (1) должен быть функцией скорости.
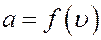
С учетом этого перепишем (1) в виде
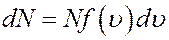 (2)
(2)
Из (2) получим
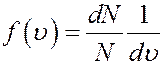 (3)
(3)
Функция f(υ) называется функцией распределения. Ее физический смысл следует из формулы (3)
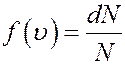 если
если 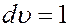 (4)
(4)
Следовательно, f(υ) равна относительной доле молекул, скорости которых заключены в единичном интервале скоростей вблизи скорости υ. Более точно функция распределения имеет смысл вероятности любой молекуле газа иметь скорость, заключенную в единичном интервале вблизи скорости υ. Поэтому ее называют плотностью вероятности.
Проинтегрировав (2) по всем значениям скоростей от 0 до 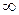 получим
получим
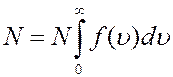 (5)
(5)
Из (5) следует, что
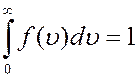 (6)
(6)
Уравнение (6) называется условием нормировки функции. Оно определяет вероятность того, что молекула имеет одно из значений скорости от 0 до 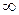 . Скорость молекулы имеет какое-нибудь значение: это событие достоверное и его вероятность равна единице.
. Скорость молекулы имеет какое-нибудь значение: это событие достоверное и его вероятность равна единице.
Функция f(υ) была найдена Максвеллом в 1859 году. Она была названа распределением Максвелла:
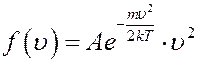 (7)
(7)
где A – коэффициент, который не зависит от скорости, m – масса молекулы, T – температура газа. Используя условие нормировки (6) можно определить коэффициент A:
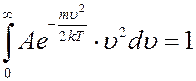
Взяв этот интеграл, получим A:
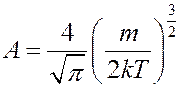
С учетом коэффициента А функция распределения Максвелла имеет вид:
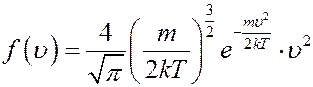 (8)
(8)
При возрастании υ множитель 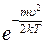 в (8) изменяется быстрее, чем растет υ2. Поэтому функция распределения (8) начинается в начале координат, достигает максимума при некотором значении скорости, затем уменьшается, асимптотически приближаясь к нулю (рис.1).
в (8) изменяется быстрее, чем растет υ2. Поэтому функция распределения (8) начинается в начале координат, достигает максимума при некотором значении скорости, затем уменьшается, асимптотически приближаясь к нулю (рис.1).
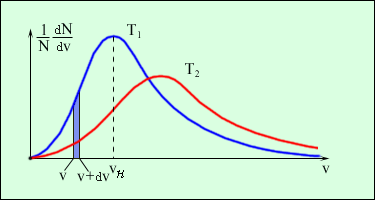
Рис.1. Максвелловское распределение молекул
по скоростям. T2 > T1
Используя кривую распределения Максвелла можно графически найти относительное число молекул 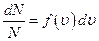 , скорости которых лежат в заданном интервале скоростей от υ до dυ (рис.1, площадь заштрихованной полоски). Очевидно, что вся площадь, находящаяся под кривой дает общее число молекул N. Из уравнения (2) с учетом (8) найдем число молекул, скорости которых лежат в интервале от υ до dυ
, скорости которых лежат в заданном интервале скоростей от υ до dυ (рис.1, площадь заштрихованной полоски). Очевидно, что вся площадь, находящаяся под кривой дает общее число молекул N. Из уравнения (2) с учетом (8) найдем число молекул, скорости которых лежат в интервале от υ до dυ
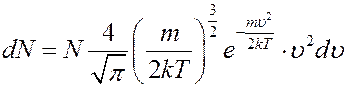 (9)
(9)
Из (8) также видно, что конкретный вид функции распределения зависит от рода газа (масса молекулы m) и от температуры и не зависит от давления и объема газа.
Под термодинамическим равновесием подразумевается такое состояние системы, когда при отсутствии внешних воздействий (изолированная система), все параметры системы остаются постоянными. В состоянии равновесия система может оставаться сколь угодно долго при отсутствии внешних воздействий. Если изолированную систему вывести из состояния равновесия и предоставить самой себе, то через некоторый промежуток времени она вернется в состояние равновесия. Этот промежуток времени называется временем релаксации. Для различных систем он различный. Если газ находится в равновесном состоянии, то распределение молекул по скоростям не изменяется с течением времени. Скорости отдельных молекул беспрерывно изменяются, однако число молекул dN, скорости которых лежат в интервале от υ до dυ все время остается постоянным.
Максвелловское распределение молекул по скоростям всегда устанавливается, когда система приходит в состояние равновесия. Движение молекул газа хаотичное. Точное определение хаотичности тепловых движений следующее: движение молекул полностью хаотично, если скорости молекул распределены по Максвеллу. Отсюда следует, что температура определяется средней кинетической энергией именно хаотичных движений. Как бы ни велика была бы скорость сильного ветра, она не сделает его «горячим». Ветер даже самый сильный, может быть и холодным и теплым, потому что температура газа определяется не направленной скоростью ветра, а скоростью хаотического движения молекул.
Из графика функции распределения (рис.1) видно, что число молекул, скорости которых лежат в одинаковых интервалах dυ, но вблизи различных скоростей υ, больше в том случае если скорость υ приближается к скорости, которая соответствует максимуму функции f(υ). Эта скорость υн называется наивероятнейшей (наиболее вероятной). Продифференцируем (8) и приравняем производную нулю:
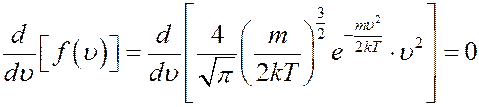
Так как 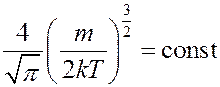 ,
,
то последнее равенство выполняется когда:
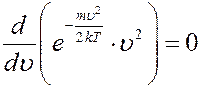
Или:
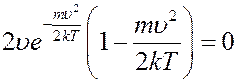 (10)
(10)
Уравнение (10) имеет три корня:
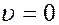 ,
, 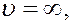 , и
, и 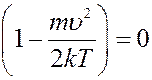
Первые два корня соответствуют минимальным значениям функции. Тогда скорость, которая соответствует максимуму функции распределения, найдем из условия:
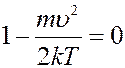
Из последнего уравнения:
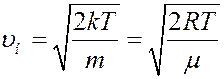 (11)
(11)
где R – универсальная газовая постоянная, μ – молярная масса.
С учетом (11) из (8) можно получить максимальное значение функции распределения
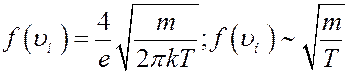 (12)
(12)
Из (11) и (12) следует, что при повышении T или при уменьшении m максимум кривой f(υ) сдвигается вправо и становится меньше, однако площадь под кривой остается постоянной (рис.1).
Для решения многих задач удобно пользоваться распределением Максвелла в приведенном виде. Введем относительную скорость:
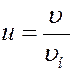
где υ – данная скорость, υн – наивероятнейшая скорость. С учетом этого уравнение (9) принимает вид:
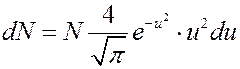 (13)
(13)
где 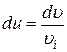 .
.
(13) – универсальное уравнение. В таком виде функция распределения не зависит ни от рода газа, ни от температуры.
Кривая f(υ) ассиметрична. Из графика (рис.1) видно, что большая часть молекул имеет скорости большие, чем υн. Асимметрия кривой означает, что средняя арифметическая скорость молекул не равна υн. Средняя арифметическая скорость равна сумме скоростей всех молекул, деленная на их число:
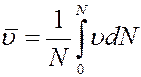
Учтем, что согласно (2)
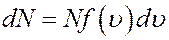
Тогда:
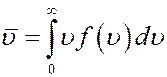 (14)
(14)
Подставив в (14) значение f(υ) из (8) получим среднюю арифметическую скорость:
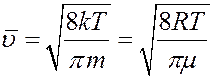 (15)
(15)
Средний квадрат скорости молекул получим, вычислив отношение суммы квадратов скоростей всех молекул к их числу:
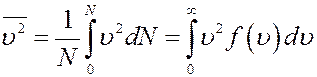
После подстановки f(υ) из (8) получим:
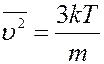
Из последнего выражения найдем среднюю квадратичную скорость:
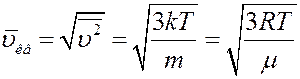 (16)
(16)
Сопоставляя (11), (15) и (16) можно сделать вывод, что 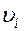 ,
, 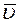 и
и 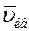 одинаково зависят от температуры и отличаются только численными значениями:
одинаково зависят от температуры и отличаются только численными значениями: 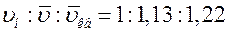 (рис.2).
(рис.2).
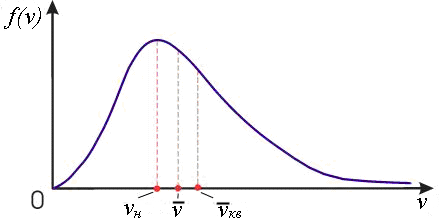
Рис.2. Распределение Максвелла по абсолютным значениям скоростей
Распределение Максвелла справедливо для газов находящихся в состоянии равновесия, рассматриваемое число молекул должно быть достаточно большим. Для малого числа молекул могут наблюдаться значительные отклонения от распределения Максвелла (флуктуации).
Первое опытное определение скоростей молекул провел Штерн в 1920 году. Прибор Штерна состоял из двух цилиндров разных радиусов, закрепленных на одной оси. Воздух из цилиндров был откачен до глубокого вакуума. Вдоль оси натягивалась платиновая нить, покрытая тонким слоем серебра. При пропускании по нити электрического тока она нагревалась до высокой температуры (~1200оС), что приводило к испарению атомов серебра.
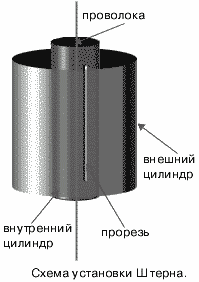
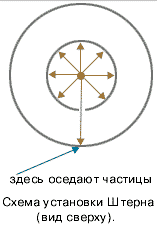
В стенке внутреннего цилиндра была сделана узкая продольная щель, через которую проходили движущиеся атомы серебра. Осаждаясь на внутренней поверхности внешнего цилиндра, они образовывали хорошо наблюдаемую тонкую полоску прямо напротив прорези.
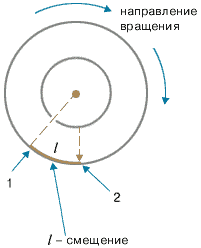
Цилиндры начинали вращать с постоянной угловой скоростью ω. Теперь атомы, прошедшие сквозь прорезь, оседали уже не прямо напротив щели, а смещались на некоторое расстояние, так как за время их полета внешний цилиндр успевал повернуться на некоторый угол. При вращении цилиндров с постоянной скоростью, положение полоски, образованной атомами на внешнем цилиндре, смещалось на некоторое расстояние l.
1) Здесь оседают частицы, когда установка неподвижна. 2) Здесь оседают частицы при вращении установки
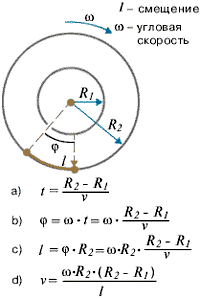
Полученные значения скоростей подтвердили теорию Максвелла. Однако опыт не был достаточно точным, полученный характер распределения молекул по скоростям был очень приблизительным.
Более точно распределение Максвелла было проверено опытами Ламмерта, Истэрмана, Элдриджа и Штерна. Эти опыты достаточно точно подтвердили теорию Максвелла.
Прямые измерения скорости атомов ртути в пучке были выполнены в 1929 году Ламмертом. Упрощенная схема этого эксперимента показана на рис. 3.
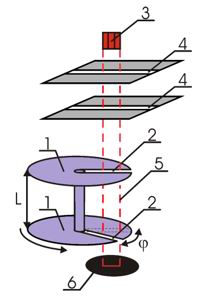
Рис.3. Схема опыта Ламмерта
1 - быстро вращающиеся диски, 2 - узкие щели, 3 - печь, 4 - коллиматор, 5 - траектория молекул, 6 – детектор
Два диска 1, насаженные на общую ось, имели радиальные прорези 2, сдвинутые друг относительно друга на угол φ. Напротив щелей находилась печь 3, в которой нагревался до высокой температуры легкоплавкий металл. Разогретые атомы металла, в данном случае ртути, вылетали из печи и с помощью коллиматора 4 направлялись в необходимом направлении. Наличие двух щелей в коллиматоре обеспечивало движение частиц между дисками по прямолинейной траектории 5. Далее атомы, прошедшие прорези в дисках, регистрировались с помощью детектора 6. Вся описанная установка помещалась в глубокий вакуум.
При вращении дисков с постоянной угловой скоростью ω, через их прорези беспрепятственно проходили только атомы, имевшие некоторую скорость υ. Для атомов, проходящих обе щели должно выполняться равенство:
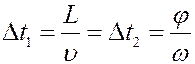
где Δt1 - время пролета молекул между дисками, Δt2 - время поворота дисков на угол φ. Тогда:
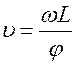
Изменяя угловую скорость вращения дисков можно было выделять из пучка молекулы, имеющие определенную скорость υ, и по регистрируемой детектором интенсивности судить об относительном содержании их в пучке.
Таким способом удалось экспериментально проверить Максвелловский закон распределения молекул по скоростям.
| <== предыдущая лекция | | | следующая лекция ==> |
| ОСНОВНЫЕ ГАЗОВЫЕ ЗАКОНЫ | | | Газ в силовом поле. Барометрическая формула. Распределение Максвелла – Больцмана. Экспериментальное определение числа Авогадро. |
Дата добавления: 2015-05-21; просмотров: 5161;
