ОСНОВНЫЕ ГАЗОВЫЕ ЗАКОНЫ
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА.
УНИВЕРСАЛЬНАЯ ГАЗОВАЯ ПОСТОЯННАЯ.
ОСНОВНЫЕ ГАЗОВЫЕ ЗАКОНЫ
Уравнения, полученные на основе МКТ, позволяют найти соотношения, которые связывают между собой макроскопические величины, определяющие состояние газа.
Физические величины, служащие для характеристики состояния газа называются параметрами состояния.
Важнейшими параметрами состояния идеального газа являются температура T, давление p, объем V.
Параметры состояния газа p, V и T не являются независимыми. Каждый из них является функцией двух других:
p = f (V, T); V = f (p, T); T = f (p, V).
Если уравнение состояния задано в явном виде, то любой параметр можно определить, зная два других.
Соотношение
,
связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением P, температурой T и количеством вещества ν.
Для этого запишем его в виде
(1)
где N – число молекул в объеме V, k – Постоянная Больцмана. Перепишем (1) в виде
. (2)
Для данной массы газа N = const, поэтому правая часть уравнения (2) будет тоже постоянная величина для данной массы газа. Тогда из (2) следует, что для данной любой массы газа будет выполняться соотношение
(3)
Полученное уравнение называется уравнением Клапейрона.
Для данной массы газа произведение давления на объем, деленное на абсолютную температуру, остается постоянным независимо от состояния, в котором находится газ.
Уравнение (2), в которое входят все три параметра состояния это уравнение состояния идеального газа. Однако в это уравнение входит число молекул N, которое невозможно измерить непосредственно. Чтобы этим уравнением можно было легко пользоваться, необходимо число молекул N заменить массой газа m, которую легко определить.
Известно, что количество вещества определяется соотношением
(3)
где N – число молекул в массе газа m, μ –молярная масса, NА - число Авогадро.
Из (3) получим
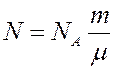(4)
С учетом (4) перепишем (2) в виде
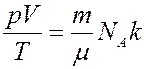(5)
В уравнение (5) входят две универсальные константы: число Авогадро и постоянная Больцмана. Очевидно, что произведение универсальных констант так же должно быть универсальной константой. Эта константа получила название универсальной газовой постоянной.
(6)
С учетом (6) перепишем (5) в виде:
(7)
Уравнение (3), устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном. В виде уравнения (7) оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.
Определим физический смысл универсальной газовой постоянной. Пусть 1 моль любого газа находится в цилиндре с подвижным поршнем. Давление газа в цилиндре p, температура T, площадь поршня S. Нагреем газ на 1K при постоянном давлении, т.е. p = const., T1 = T, T2 = T+1. При этом поршень переместится на расстояние dl (рис.1).
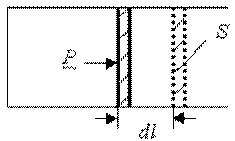
Рис.1.
Сила, действующая со стороны газа на поршень
,
т.к. p = const. Следовательно, работа расширения газа из состояния 1 в состояние 2
С учетом F
Учтем, что Sdl = dV – изменение объема газа при нагревании. Тогда:
Запишем уравнения Клапейрона-Менделеева для двух состояний газа с учетом того, что ν = 1моль и вычтем из второго первое
Следовательно, работа расширения газа
Универсальная газовая постоянная численно равна работе расширения, которую выполняет 1 моль газа при его нагревании на 1K при постоянном давлении.
Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах p,V) в виде некоторой линии, каждая точка которой представляет равновесное состояние.
Интерес представляют процессы, в которых один из параметров (p, V или T) остается неизменным. Такие процессы называются изопроцессами.
Изотермический процесс (T = const.).
Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. Из уравнения (7) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:
(8)
На диаграмме (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гипербол p ~ 1 / V, которые называются изотермами. Изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис. 2). Уравнение изотермического процесса было получено из эксперимента английским физиком Р. Бойлем (1662 г.) и независимо французским физиком Э. Мариоттом (1676 г.). Это уравнение называют законом Бойля–Мариотта. (8) – уравнение изотермы.
Рис.2. Семейство изотерм: T3 > T2 > T1.
Сжимаемость газа при изотермическом процессе характеризуется изотермическим коэффициентом сжимаемости α, который определяется как относительное изменение объема, изменяющее давление на единицу.
где dV изменение объема газа, которое изменяет давление на dp. Продифференцируем уравнение Клапейрона–Менделеева с учетом того, что T = const.
После дифференцирования получим
Из этого уравнения
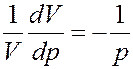
Следовательно
Изотермический коэффициент сжимаемости идеального газа равен обратной величине его давления. Знак минус указывает на то, что увеличение объема приводит к уменьшению давления и наоборот.
Изобарный процесс (p = const)
Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p. Из уравнения (7) следует, что уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:
(9)
На диаграмме (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3), которые называются изобарами. Уравнение (9) – уравнение изобары.
Рис.3.Семейство изобар: p3 > p2 > p1.
Для данной массы газа при постоянном давлении объем газа прямо пропорционален его абсолютной температуре.
Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Ж. Гей-Люссаком (1862 г.). Уравнение изобарного процесса называют законом Гей-Люссака.
Коэффициент объемного расширения газа при постоянном давлении равен относительному изменению объема газа при изменении температуры на один Кельвин.
Продифференцируем уравнение Клапейрона–Менделеева с учетом того, что p = const.
После дифференцирования получим
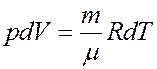
Из последнего уравнения:
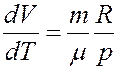
Из уравнения Клапейрона–Менделеева
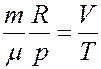
Из двух последних уравнений
Следовательно
Отсюда следует, что коэффициент объемного расширения идеального газа равен обратной величине абсолютной температуры.
Так при 0оС он равен
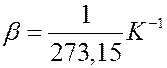
Изохорный процесс (V = const)
Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.
Как следует из уравнения (7) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p ~ T или
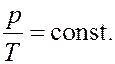(10)
На диаграмме (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 4).
Рис.4. Семейство изохор: V3 > V2 > V1.
Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Уравнение изохорного процесса (10) называется законом Шарля.
Уравнение изохорного процесса может быть записано в виде:
где p0 – давление газа при T = T0 = 273,15 К (т. е. при температуре 0 °С). Коэффициент χ, равный (1/273,15) К–1, называют температурным коэффициентом давления.
Закон Авогадро (1811 г.)
Запишем основное уравнение МКТ (1) для двух разных газов, которые занимают одинаковые объемы, при одинаковых температурах и давлениях
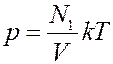
Из этих уравнений видно, что N1 = N2. При одинаковых давлениях и температурах в равных объемах любых газов содержится одинаковое число молекул. Это утверждение называется законом Авогадро.
Если температура газа равна T0 = 273,15 К (0°С), а давление p0 = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V0, равный
V0 = 0,0224 м3/моль = 22,4 дм3/моль.
Закон Дальтона (1803г.)
Пусть в сосуде объемом V находится смесь невзаимодействующих газов. Для этой смеси основное уравнение МКТ (1) примет вид
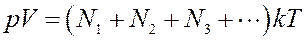
где N1,N2, N3 … число молекул компонентов смеси. Очевидно, что
где N – общее число молекул в сосуде. Давление смеси газов в сосуде
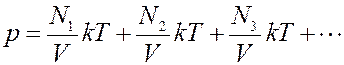
Из этого уравнения видно, что каждая группа молекул оказывает давление на стенки сосуда, которое не зависит от давления других групп молекул. То есть
, 
, 
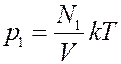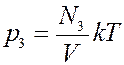и т.д.
Тогда
где p1, p2, p3 – парциальные давления.
Парциальным давлением называется давление, которое создается каждым из компонентов смеси в данном объеме в отсутствие других компонентов смеси.
Давление смеси невзаимодействующих газов равно сумме парциальных давлений компонентов составляющих эту смесь – закон Дальтона.
Дата добавления: 2015-05-21; просмотров: 1452;