ПРОГНОЗИРОВАНИЕ И РАСПОЗНАВАНИЕ ОБРАЗОВ

Кардинальное значение для психодиагностики имеет проблема прогнозирования. Существует точка зрения, разделяющая психоди­агностику и так называемую психопрогностику (Забродин Ю. М., 1984). Это указывает на самостоятельное значение проблемы прогно­зирования.

В действительности, любая психодиагностика служит прогнози­рованию - на больших или меньших отрезках времени. То, что назы­вается диагностикой текущего состояния объекта, имеет следующий смысл. В технике сконструированный агрегат подвергают стендовым испытаниям. Полученные результаты приписывают текущему состо­янию объекта, имея в виду, что выключенный агрегат до его эксплуа­тации в реальных условиях уже не будет изменяться сколь-нибудь су­щественным образом. При этом подразумевается, что именно при работе включенного агрегата может измениться его состояние, в ча­стности, выход из допустимого режима.

В психологии дело, конечно же, обстоит по-другому. И перенос подразумеваемых, имплицитных представлений из технической ди­агностики в психодиагностику неправомерен, как, впрочем, непра­вомерен такой перенос уже и по отношению к медико-биологичес­кой диагностике человеческого организма. Организм человека, его психика - это не агрегат, который произвольно можно выключить на период от тестирования до реального испытания. Все это время человек продолжает жить, активно взаимодействовать со средой. Даже в изоляции, даже во сне мозг человека проделывает большую работу, переводя полученную информацию из одних отделов памя­ти в другие (Касаткин В. Н., 1967). Все это означает, что принцип статистической экстраполяции результатов психодиагностического измерения нельзя считать оправданным без проведения специаль­ных проверок.

Когда психолог по результатам тестирования регистрирует у не­которого индивида А показатель Х_а, а у некоторого индивида В пока­затель Х_b, так что Х_a> Х_b, то из этого вовсе не следует автоматичес­ки, что соотношение Х_a> Х_b сохранится в течение следующей недели, месяца, года. Для принятия стратегии экстраполяционного статистического прогноза требуется предварительно произвести эмпиричес­кое измерение надежности - устойчивости (ретестовой надежности) на заданном промежутке времени.

При этом важна не только длина отрезка времени между двумя изме­рениями, но и его заполненность теми или иными значимыми для инди­вида событиями. Приведем простой пример. Организовано психологи­ческое обследование абитуриентов вуза. Психологи пытаются измерить уровень интереса поступающих к избранной специальности Однако они применяют «лобовые» методики опроса, не защищенные от преднаме­ренной фальсификации (абитуриенты сознательно, или даже бессозна­тельно, будут искажать результаты в сторону повышенного интереса - чтобы произвести благоприятное впечатление). Фальсификация здесь - только один из возможных источников некорректности статистического прогноза. Для эмпирического измерения силы этого артефакта не обяза­тельно проводить повторное измерение через несколько лет. Имеет смысл провести повторное обследование по той же методике всех студентов, сразу же после их зачисления на первый курс. Если возникнет слишком много перестановок типа Х_а < Х_b, то ранговая корреляция «тест -ретест» окажется слишком слабой, и это доказывает неправомерность использо­вания «лобовой» методики для статического прогноза. Другой возмож­ный источник нестабильности ранговой шкалы (порядковой шкалы тес­та) обусловлен в данном примере зависимостью уровня интереса к пред­метной области от уровня знаний о предмете. В ходе обучения в вузе студенты приобретают более детальные знания о предмете, о своей ус­пешности в освоении специальности, и от этого уровень интереса может существенно изменяться. Конечно, этот фактор - в отличие от фактора фальсификации - действует на более длительных промежутках време­ни. И здесь опять же требуются специальные измерения ретестовой ус­тойчивости для применения статического прогноза.

Приведенный выше пример показывает, что в некоторых случаях целесообразно начинать решать проблемы психопрогностики без вся­кого привлечения внешней по отношению к тесту критериальной ин­формации, т. е. средствами проверки надежности, но не средствами проверки валидности. Если уже таким способом будет получен отри­цательный результат, то заведомо будет получен и для измерения ва­лидности статического прогноза (вспомним основной принцип: валидность методики не превышает ее надежность).

Однако надежность лишь необходимое, но, естественно, недоста­точное условие прогностической валидности. Можно убедиться в высо­кой устойчивости тестового показателя на длительных промежутках вре­мени, но из этого вовсе не следует, что будут получены значимые линей­ные корреляции этого показателя с требуемым критерием валидности -эффективности.- корреляции, оправдывающие статический прогноз.

Как правило, на основе диагностики принимаются решения, кото­рые соотносятся между собой как события на шкале наименований или на шкале порядка. Каким образом учитываются сегодня при приеме в вуз показатели школьной успеваемости абитуриентов? Существуют три варианта, три градации, соотносимые друг с другом по шкале порядка: выпускникам школы - медалистам предоставляются льготные условия (при успехе на первом экзамене от остальных вступительных экзаме­нов медалист освобождается), лица с удовлетворительным средним баллом допускаются к конкурсным вступительным экзаменам и сдают все экзамены; наконец, лица с неудовлетворительным средним баллом могут вообще не допускаться к вступительным экзаменам. На этом при­мере видно, что средний балл аттестата используется как некоторый показатель «теста», в соответствии с которым абитуриентов разделяют на три категории, по отношению к которым неявно применяется «по­рядковый» прогноз: предполагается, что медалисты будут успешнее обычных выпускников школ, а обычные выпускники - успешнее тех, кто учился в школе очень слабо.

«Порядковый» прогноз сохраняет свою эффективность не только в статических условиях, но и в условиях таких динамических измене­ний объектов прогнозирования, при которых порядковая структура оказывается неизменной. Предположим, что в_: ходе обучения в вузе все студенты по мере более глубокого ознакомления с предметом ис­пытывают нарастающий интерес к своей специальности, но если по­рядковая структура сохраняется (Х_а продолжает превышать X_b, несмот­ря на то что X_b приближается к Х_а), то «порядковый» прогноз все рав­но остается корректным.

Линейные и порядковые прогностические стратегии на практике применяются не к одномерным, а к многомерным данным. Среди математических моделей прогнозирования до сих пор наибольшей популярностью пользуются относительно простые (а иногда и нео­правданно упрощенные) регрессионные модели.

При этом для многомерного случая задача психометриста сводится к построению уравнения множественной регрессии:

Y= ß₁X₁+ ß₂X₂…..+ ß_iX_i+ ß_kX_k (3.5.1)

где Y- прогнозируемая переменная (критерий прогностической ва-лидности);

X_i - значение i-го тестового показателя из рассматриваемой бата­реи тестовых показателей;

ß_i, - значение весового коэффициента, указывающего, на сколько (в единицах стандартных отклонений) изменяется прогнозируемая переменная при изменении тестового показателя X_i.

Для составления указанного уравнения требуется произвести «уп­реждающее» измерение тестовых показателей по отношению к критериальному показателю Y, измерение которого производится по ис­течении некоторого отрезка времени 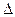T, называемого в прогнозиро­вании периодом упреждения.

Общая эффективность прогноза на основе регрессионного урав­нения оценивается с помощью подсчета коэффициента множествен­ной корреляции R² (Суходольский Г. В., 1972) и последующей оценки его значимости по критерию Фишера:

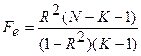(3.5.2)

где 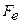- эмпирическое значение статистики Фишера со степенями сво­боды V₁ = k и У₂ = N-k;

N— количество индивидов;

k - количество тестовых показателей.

Не следует забывать, что основой применения этой модели про­гноза является экстраполяция - предположение о том, что на новом отрезке времени 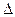T’ будут действовать те же тенденции связи пере­менных, что и на отрезке 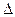T, на котором прежде измерялись весовые коэффициенты ß_i. Не следует также забывать, что корректность про­гноза обусловлена периодом упреждения: для больших (или меньших) 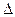T использование уравнения (3.5.1) может оказаться некорректным.

Прогностические возможности указанного метода ограничены однократностью измерения тестовых показателей .X₁, Х₂ ..., X_k. В силу однократности измерения этот метод оказывается эффективным опять-таки только по отношению к самым универсальным и статическим показателям (таким, например, как интегральные свойства темпера­мента или нервной системы), обеспечивающим очень грубый, веро­ятностный, приближенный прогноз.

В некоторых случаях эффективность этого метода может суще­ственно повыситься, если использовать хотя бы двукратное (с неболь­шим интервалом в две-три недели) измерение системы показателей Х₁ Х₂,..., X_k. Уже таким способом можно, например, учесть вклад фак­тора «усвоение знаний» в прогнозирование мотивационной вовлечен­ности (уровня интереса) студента в свою специальность. Повторное измерение (например, через месяц после начала обучения в вузе) по­зволяет выявить, в каком направлении действует фактор «усвоение знаний» в своем влиянии на уровень интереса данного студента: мо­жет оказаться, что в результате разнонаправленного действия этого фактора немало пар студентов уже через месяц поменяются местами в ранговом ряду по уровню интереса (Х_а< Х_b). В этом случае в урав­нение (3.5.1) целесообразно ввести не статический показатель X_i a простейший динамический показатель 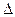Х_i, = 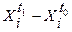. Кроме того, не исключена возможность одновременного использования в уравнении (3.5.1) и статических X_i. и динамических 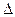Х_i. показателей; тогда разра­ботанная модель прогноза будет учитывать как достигнутый уровень (экстраполировать статику), так и намечающиеся тенденции (экстра­полировать тенденции).

Приведем еще один содержательный пример. Многочисленные эмпирические исследования по прогнозированию супружеской со­вместимости (Обозов Н. Н., 1979) показали неудовлетворительно низкий уровень надежности прогноза на основе таких показателей, как однократно измеренный уровень сходства (темперамента, моти­вов, интересов, ценностных ориентации) или взаимодополнитель­ности психических свойств будущих супругов. Но эту надежность можно существенно повысить, если ввести в уравнение (3.5.1) по­казатели типа 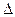Х.. В данном случае содержательно-психологичес­кий смысл этих показателей будет заключаться в следующем: они указывают на то, в каком направлении действует на уровень сход­ства (совместимости) опыт взаимодействия будущих супругов. По­тенциально несовместимые супруги в ходе взаимодействия (за период помолвки), как правило, дивергируют в своих показателях (на­пример, имеющиеся незначительные акцентуации характера взаим­но усиливаются). И наоборот, потенциально совместимые супруги могут очень быстро конвергировать: оказывается достаточным про­ведение одного-двух обсуждений с участием психолога по спорным вопросам, чтобы сблизиться в представлениях о желаемом семей­ном укладе и образе жизни.

Более сложные математические методы прогнозирования (напри­мер, учитывающие циклическую динамику объектов) пока еще редко используются в психодиагностике, так как требуют частых многократ­ных измерений системы тестовых показателей, что оказывается не­возможным по чисто практическим причинам. Тем не менее уже се­годня можно твердо констатировать недостаточность линейных мо­делей прогнозирования. Для ознакомления с рядом других подходов к прогнозированию мы рекомендуем психологам обратиться к руко­водству «Рабочая книга по прогнозированию» (М., 1982).

Остановимся теперь более подробно на подходе, который ныне представляет собой реальную альтернативу ограниченным линей­ным статистическим моделям и позволяет строить эффективный прогноз для более сложных зависимостей между прогнозируемыми (зависимыми) и прогнозирующими (независимыми) переменными. Этот подход, по традиции, принято называть распознаванием обра­зов, так как разработка его математического аппарата была во мно­гом стимулирована инженерными задачами конструирования искус­ственных систем зрения, слуха, других органов чувств (Распознава­ние образов. М., 1970).

В психодиагностике роль «элементарных сенсорных данных» выполняют первичные тестовые показатели X₁ Х₂,..., X_k, а роль «об­раза» (выходного сигнала системы) - соответствующая диагностичес­кая категория. Таким образом, по существу, распознавание образов[19] и есть диагностика в широком смысле.

Поясним специфику подхода на простейшем схематическом при­мере. Пусть Р_у -вероятность такого типового критерия оценки студен­тов, как успеваемость, Х₁ - уровень интереса к специальности, выяв­ленный у абитуриента, Х₂ - уровень его знаний о специальности.

На рис. 16 точки X₁ = 0 и Х₂ = 0 - медианные значения соответ­ствующих тестовых показателей. В данном упрощенном примере в статусе «образа» выступает каждый из четырех квадрантов диагнос­тического пространства. Для предсказания Р_у мы не можем постро­ить линейной комбинации Х₁ и Х₂, какие бы коэффициенты ß₁, и ß₂ мы ни взяли. Для предсказания Р_y мы должны зафиксировать попадание индивида в заданную область пространства параметров. «Образ», или диагностическая категория, и есть на геометрическом языке опреде­ленная область в пространстве параметров.

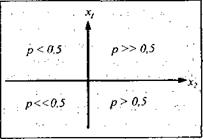
Рис. 16. Зависимость вероятности критериального события р и диагностических параметров X₁ и Х₂

С точки зрения распознавания образов, предварительная задача диагностики (предваряющая практические задачи) – определить границы диагностических категорий - областей в пространстве парамет­ров, которым эмпирически корректно могут быть приписаны некоторые пороговые (качественно специфичные) значения прогнозируемого критериального показателя. Это задача построения «разделяющего правила» (или «решающего правила»). Точность такого разделения и предопределяет прогностическую валидность методики на данной совокупности испытуемых в данной диагностической ситуации.

Репрезентативность выборки при этом определяется степенью изменения точности разделения при увеличении совокупности обсле­дованных. Влияние того или иного параметра на точность разделе­ния определяет «вес», с которым входит данный параметр в задачу диагностики.

Построение формальной процедуры разделения может произво­диться по-разному. В простейшем случае - это сравнение тестового показателя с некоторым порогом. В более сложных случаях применя­ются методы дискриминантного анализа, позволяющие описывать «разделяющие правила» (границы диагностических областей в про­странстве параметров) в виде сложных функций сразу от нескольких параметров.

Применение определенного метода для решения задачи построе­ния системы диагностических категорий определяется несколькими факторами: во-первых, это соответствие допущений, положенных в основу алгоритма, содержательным представлениям о психологичес­кой типологии индивидов в рамках рассматриваемой системы психо­диагностических параметров; во-вторых, это степень полноты имею­щейся информации для эффективной «остановки» алгоритма, обес­печивающей оптимальное решение задачи за приемлемое время.

Под полнотой информации здесь, имеется в виду наличие доста­точно многочисленных групп индивидов, четко и однозначно класси­фицированных по заданной системе критериев. В этом случае пост­роение решающего правила сводится к применению какого-либо ал­горитма автоматической классификации, приспособленного к работе с заданными классами. Если же критериальные классы представлены неполно - всего несколькими представителями, для которых при этом не всегда известны все значения необходимых параметров, - то воз­никает ситуация, требующая применения так называемых эвристи­ческих алгоритмов (более подробно о применяемых алгоритмах клас­сификации см. кн.: Типология и классификация в социологических исследованиях. М., 1982).

Остановимся на одном из методов распознавания, получившем применение в психодиагностике, — на семействе алгоритмов вычис­ления оценок (АВО), предложенном Ю. И. Журавлевым и его учени­ками (1978).

Основную задачу распознавания образов можно сформулировать как задачу отнесения объекта 5 к одному или нескольким классам К₁ К₂,..., К_i на основе информации о классах I (K₁), (К₂),..., I (К_i), ин­формации об объекте I(S) и предположения о близости объекта к клас­су. Другими словами, задачу распознавания можно сформулировать как задачу определения того, обладает ли объект определенными свой­ствами.

В основе АВО лежит принцип частичной прецедентности: бли­зость объекта к классу тем больше, чем больше частей в его описании «похожи» на соответствующие части в описаниях' объектов, чья принадлежность классу известна. Например, в одном из вариантов АВО (Зеличенко А. И., 1982) функция близости объекта S к классу К опре­деляется так:

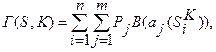(3.5.3)

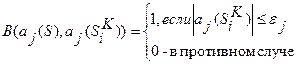
где 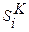- i-й объект, принадлежность которого к классу К уже известна;

a_i (S) - i-й элемент (параметр) в описании объекта;

P₁ - его вес;

ε_j - i-й порог.

После того как вычислены Г(S₁ K₁,), ... , Г(S₁ K₁,) на основании некоторого решающего правила (зависящего от вектора параметров 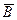, принимается решение о принадлежности объекта к одному или нескольким классам К₁, ..., К₁ В задачах психодиагностики S- это испытуемый.

Таким образом, каждый вариант АВО определяется набором зна­чений параметров. В нашем случае- это векторы 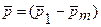, 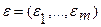. Если информация об объекте S представлена в виде I(S) = (а_1,..., а₂), то элемент вектора опорных множеств ω_j(S) = а_i, a ε_j -j-й порог.

В качестве примера решающего правила можно привести следу­ющее (линейное пороговое решающее правило):

объект S принадлежит к классу K_t если

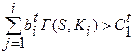(3.5.4)

объект S не принадлежит к классу K_t если

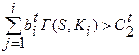(3.5.5)

в остальных случаях -отказ от распознавания принадлежности объек­та S к классу K_t.

В работе алгоритмов распознавания вообще и АВО в частности мож­но выделить два этапа: обучение и собственно распознавание. На этапе обучения, как уже говорилось, происходит настройка алгоритма, т. е. выбор таких его параметров, которые обеспечивают оптимальное в нег котором смысле распознавание объектов обучающей выборки (объек­тов, принадлежность которых к классам К₁, ... ,K_i, известна). На этапе собственно распознавания происходит отнесение к классам K₁,..., К_i, тех объектов, принадлежность которых к классам априорно неизвестна.

Точность распознавания на этапе обучения измеряется полнотой и адекватностью распознавания эталонных объектов. Наряду с понятием «точность» (абсолютная отделимость) иногда удобно использовать по­нятие относительной отделимости объектов обучающей выборки, при­надлежащих к различным классам. В случае, когда распознавание ведется для двух классов (например, в профориентации - для дифференци­ального прогноза успешности оптанта в одной из двух профессиональ­ных областей), относительную отделимость можно определить как

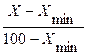(3.5.6)

где X - точность при обучении (выраженная в процентах), a 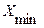-минимальная возможная точность обучения (совпадает с долей объек­тов в наибольшем классе от общего объема обучающей выборки). На этапе собственно распознавания точность характеризует главным об­разом репрезентативность обучающей выборки (выборки валидизации). Чем выше репрезентативность, тем больше совпадают показа­теле точности на этапах обучения и собственно распознавания.

Использование АВО кроме решения задачи распознавания позволяет получить следующую информацию:

1. Информационные веса отдельных элементов (параметров) опи­сания объектов. Эти веса измеряются через изменение точности рас­познавания при исключении соответствующих параметров из описа­ния эталонных объектов:

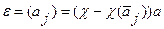
(3.5.7)

где X - точность распознавания при Р_j = 1; X( 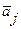) - точность распозна­вания при Р. = 0, а а - нормирующий множитель. Информационные веса интерпретируются как мера прогностической важности параметров.

2. Оптимальные значения порогов 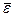, т. е. значения 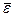, обеспечи­вающие наивысшую точность распознавания. Эти значения порогов в нашем случае можно .интерпретировать как чувствительность мето­дики; ε_j - своего рода дифференциальный порог на шкале тестового показателя a_j определяющий переход индивида из одной диагности­ческой категории в другую. Пусть на этапе разработки теста (тесто­вой батареи) была обследована группа из К человек, про которых из­вестно, что k₁ из них относится к одному классу, а К₂ - к другому, К = К₁ + К₂. Выбрав случайным образом из этой группы М (М<<К) многомерных описаний, проводим на них процедуру обучения алго­ритма. Точность обучения характеризует валидность теста. После это­го применяем процедуру собственно распознавания (по выработан­ному решающему правилу) для остальных К-М описаний. В резуль­тате этой процедуры мы определяем принадлежность респондентов (испытуемых) к этим классам. Сравнивая полученные результаты с эталонными данными о принадлежности испытуемых к классам, мы определяем точность самого распознавания. Если эта точность близ­ка к точности обучения, то наша пилотажная выборка объемом М может быть признана репрезентативной для обучения. Теперь можно переходить к задаче определения информационных весов.

* * *

Для эффективного использования алгоритмов распознавания по отношению к многомерным тестовым системам (при K>3), как пра­вило, требуется использование компьютера.

При решении задач небольших размерностей (по количеству па­раметров) иногда психолог может быстрее найти решающее прави­ло, применяя собственные способности зрительной системы (очень мощные) к визуально-геометрической группировке объектов. В про­странстве параметров диагностические, классы выглядят как «сгуще­ния», некие «облака» из точек, изображающих испытуемых. В этом случае при наличии априорной информации о принадлежности ин­дивидов к классам удобно изображать точки из различных классов разными цветами (хуже - квадратиками, кружками, треугольниками). В этом случае «решающее правило» легко «увидеть» как некую вооб­ражаемую линию (прямую или кривую), разделяющую точки разного цвета (рис. 17). Точность диагностики в данном случае можно оценить по количеству точек, попавших при данном решающем правиле в «чужую» половину пространства параметров.

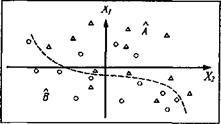
Рис.17. Разделение двух классов объектов (изображены кружками и треугольниками) в пространстве двух параметров X₁, и Х₂

Точность правила, изображенного на рис. 17, равна:

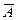
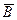
A

B

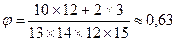
Здесь в четырехклеточной матрице сопряженности по строкам за­дано попадание объекта в один из априорных классов А (треугольни­ки на рис. 17) или В (кружочки на рис. 17), а по столбцам - попадание объектов в один из апостериорных классов, образованных примене­нием решающего правила, - 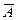(слева от критериальной линии) или 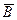(справа от критериальной линии). Как указано выше, для статис­тической оценки точности может быть использован фи-коэффициент, связанный по известной формуле с критерием хи-квадрат.