Общие условия фазового равновесия. Правило фаз Гиббса.

Любая закрытая система, находящаяся в равновесии при постоянных давлении и температуре, характеризуется соотношением: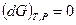

Для системы переменного состава (смотри (III, 55)):

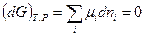(IV, 11)

Если при постоянных Р и Т из фазы 1 в фазу 2 переходит 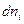молей i-ого компонента, то

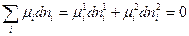(IV, 12),

где верхний индекс относится к фазе, а нижний индекс – к компоненту.

При переходе 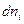молей i-ого компонента из фазы 1 в фазу 2 его количество в одной из фаз убывает, а в другой фазе увеличивается на ту же самую величину, следовательно, 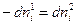. Тогда уравнение (IV, 12) можно записать в следующем виде:

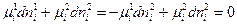
или (IV, 13)

Таким образом, химический потенциал i-ого компонента в фазе 1 равен химическому потенциалу в фазе 2.

Обобщая этот результат на все фазы и все компоненты гетерогенной системы, получим условие равновесия:

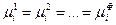(IV, 14),

где Ф – число фаз.

Таким образом, гетерогенная система будет находиться в состоянии равновесия при выполнении равенств (IV, 14) и ряда тождеств:

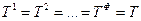
В 1876 г. Гиббс вывел простую формулу, связывающую число фаз (Ф), находящихся в равновесии, число компонентов (К) и число степеней свободы (С) системы. При равновесии должны быть выполнены следующие условия:

давление (Р) и температура (Т) одинаковы во всех точках системы,

химический потенциал ( 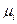) каждого i-ого компонента одинаков во всех фазах.

Рассмотрим равновесную систему из Ф фаз и К компонентов. Состав каждой фазы можно определить с помощью (К-1) концентраций, поскольку все концентрации связаны условием: 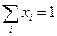, где 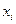- мольная доля i-ого компонента. Общее число переменных, характеризующих систему, равно 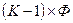концентраций плюс 2 (температура и давление):

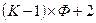(IV, 15)

Если одна из этих переменных (температура или давление) поддерживается постоянной, то число независимых переменных составит 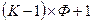. Если же на систему действует, например, внешнее магнитное поле, то общее число независимых переменных увеличится и составит .

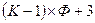Часть переменных связана уравнениями, вытекающими из условий равновесия (смотри (IV, 13)):

…………………

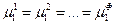
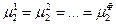
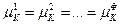
Общее число таких уравнений равно числу строк (оно соответствует числу компонентов К), умноженному на число равенств в строке ( )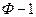

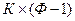(IV, 16)

Если число независимых переменных равно числу уравнений, их связывающих, то каждая независимая переменная принимает некоторое строго определенное значение и вся система может существовать только при этом единственно возможном сочетании значений температуры, давления и концентраций компонентов во всех фазах.

Если же число уравнений меньше числа независимых переменных, то их разность, которую мы определили как число термодинамических степеней свободы (С) представляет собой число переменных, которым можно придавать произвольные значения при имеющемся числе уравнений, а следовательно, и при данном числе фаз, т.к. число уравнений определяется числом фаз.
Число термодинамических степеней свободы С равно общему числу переменных (IV, 15) минус число уравнений (IV, 16), связывающих эти переменные: .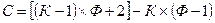

Раскрывая скобки и группируя слагаемые, получим правило фаз Гиббса:

С = К 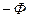+ 2

Согласно этому правилу, чем больше компонентов в системе, тем больше степеней свободы.

Для любой системы число фаз максимально, когда С = 0.

Для однокомпонентной системы К = 1 и максимальное число фаз Ф = 3.

Для двухкомпонентной системы К = 2 и максимальное число фаз Ф = 4.

Правило фаз Гиббса устанавливает общую закономерность, которой подчиняются гетерогенные системы, состоящие из любого числа фаз и любого числа компонентов.