От температуры и давления.

Полученные сведения о равновесии можно дополнить, установив зависимость константы равновесия от температуры и давления. Дифференцирование уравнения (4.93) по температуре дает:

. (4.94)

Полученное выражение и значение А_Р из уравнения (4.93) необходимо ввести в уравнение Гиббса - Гельмгольца:

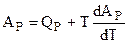
и получить

,

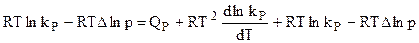откуда после упрощений:

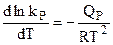. (4.95)

По аналогии:

. (4.96)

Или, учитывая соотношения и :

и

Полученные уравнения вида (4.95) и (4.96) - это уравнения изобары и изохоры химической реакции, устанавливающие зависимость константы равновесия химической реакции от температуры.

Интегрирование уравнений (4.95) и (4.96) в обобщенной форме их записи позволяет получить точное решение в виде:

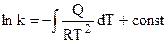. (4.97)

Если предположить, что Q f (T), то решение уравнений (4.95) и (4.96) выглядит:

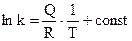. (4.98)

Из (4.98) видно, что 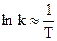, причем, если Q > 0 (экзотермическая реакция), то с ростом температуры значение k уменьшается, а если Q < 0 (эндотермическая реакция), то при увеличении температуры величина k, наоборот, увеличивается.

Сделанные выводы представляют собой частный случай принципа Ле-Шателье (или принцип подвижного равновесия), который позволяет в простейших случаях предвидеть направление течения химической реакции. Согласно этому принципу, изменение внешних условий (Т и Р) термодинамической равновесной системы вызывает в ней процессы, противодействующие произвольному изменению.

Например для реакций вида:

N₂ + O₂ 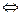2NO - 180,0 кДж,

2NО + O₂ 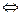2NO₂ + 111,3 кДж

повышение температуры сдвинет первое равновесие в сторону образования NO, а второе равновесие - в сторону диссоциации NО₂.

Константа равновесия k_P пропорциональна функции 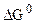, но стандартная функция энергия Гиббса определяется при строго фиксированном давлении. Следовательно, некорректно обсуждать изменение k_P при изменении давления для случая идеальных газов. Таким образом при постоянной температуре:

. (4.99)

Но это вовсе не означает, что при изменении давления количество веществ, находящихся в равновесии не изменяется. Поэтому изменение давления влияет на k_N реакции. Из уравнения (4.90):

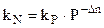
и затем:

.

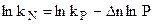Отсюда после дифференцирования при постоянной температуре:

.

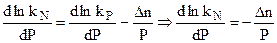Используя уравнение состояния идеального газа PV = nRT и считая Р и Т постоянными: Р V = nRT. Подставляя в полученное уравнение k_N = f (P), можно получить уравнение:

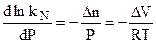, (4.100)

называемое уравнением Планка.

Если химическая реакция сопровождается уменьшением количества вещества ( n < 0), то 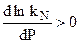, и с увеличением давления в системе равновесие смещается в сторону конечных продуктов химической реакции, что обеспечивает большую полноту превращения исходных продуктов химической реакции в конечные.