Методы анализа основной тенденции динамического ряда.
Укрупнение интервалов – это один из самых простых способов определения тренда. Он основан на укрупнении периодов времени, к которым относятся уровни изучаемого динамического ряда. Например, ряд, содержащий данные о месячном выпуске продукции, можно заменить рядом квартального выпуска продукции. При суммировании уровней или при нахождении средних по укрупненным интервалам отклонения в уровнях, которые обусловлены случайными причинами, взаимопогашаются, сглаживаются и более четко проступает основная тенденция ряда динамики. Недостатком данного ряда является то, что укрупненный ряд будет короче исходного, а это означает потерю информации.
Метод ступенчатой средней: первоначальный ряд заменяется другим, уровни которого являются средними значениями для исходного ряда.
Метод скользящей (подвижной) средней: суть состоит в том, что вычисляется средний уровень из определенного числа (четных – для четного количества уровней в ряду, нечетных – для нечетного количества уровней в ряду) первых по счету уровней, затем находится среднее из того же числа уровней, но начиная со второго по счету, затем - начиная с третьего и далее. Средняя «скользит» по динамическому ряду, сдвигаясь на один уровень. Недостатком данного способа, как и метода укрупнения интервалов, является то, что выравненный ряд будет короче исходного, поэтому часть информации теряется. Пример: трехчленная скользящая средняя для динамического ряда, в котором нечетное количество уровней.
| 100 | - | |
| 110 | ||
| 150 | ||
| 163,3 | ||
| 196,7 | ||
| - |
Для того чтобы получить количественную модель, выражающую общую тенденцию изменения уровней ряда динамики во времени, применяют аналитический способ выравнивания. В этом случае реальные (исходные) уровни ряда заменяются теоретическими уровнями. Теоретические уровни рассчитываются как функции времени:
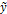 (t) = f(t)
(t) = f(t)
где 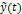 - теоретические уровни динамического ряда, найденные по уравнению на соответствующие моменты времени. Модель должна наилучшим образом аппроксимировать основную тенденцию (тренд) изучаемого ряда динамики. Подбор такой адекватной модели и есть главная задача аналитического метода. Основанием для выбора модели может быть содержательный анализ существа развития изучаемого явления. Можно использовать результаты предыдущих исследований в данной области. Некоторые виды моделей, часто применяемые для аналитического выравнивания:
- теоретические уровни динамического ряда, найденные по уравнению на соответствующие моменты времени. Модель должна наилучшим образом аппроксимировать основную тенденцию (тренд) изучаемого ряда динамики. Подбор такой адекватной модели и есть главная задача аналитического метода. Основанием для выбора модели может быть содержательный анализ существа развития изучаемого явления. Можно использовать результаты предыдущих исследований в данной области. Некоторые виды моделей, часто применяемые для аналитического выравнивания:
1) линейная 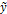 (t) = a*t + b;
(t) = a*t + b;
2) квадратичная парабола 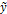 (t) = a1*t2 + a2*t + b;
(t) = a1*t2 + a2*t + b;
3) кубическая парабола 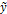 (t) = a1*t3 + a2*t2 + a3*t + b;
(t) = a1*t3 + a2*t2 + a3*t + b;
4) показательная 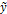 (t) = b*at;
(t) = b*at;
5) экспоненциальная 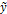 (t) = b*
(t) = b* 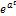 ;
;
6) логарифмическая парабола 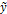 (t) = b*a1t *
(t) = b*a1t * 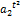 ;
;
7) гиперболическая 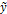 (t) =
(t) = 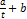 .
.
Оценка параметров (a, b) выбранной модели, как правило, осуществляется по методу наименьших квадратов (МНК). Например, система нормальных уравнений (после математических преобразований в результате применения метода МНК) для оценки параметров прямой 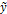 (t) = a*t + b имеет вид
(t) = a*t + b имеет вид
n*b + a 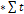 =
= 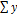 ;
;
b* 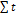 + a*
+ a* 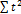 =
= 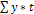 .
.
В статистической практике применяется упрощенный расчет параметров уравнения, который заключается в переносе начала координат на середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, причем сумма t равна будет нулю:
- если число членов ряда было нечетное, то t = -3,-2,-1,0,1,2,3
- если число членов ряда было четное, то t = -5,-3,-1,1,3,5
и система нормальных уравнений примет вид:
n*b = 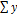 ;
;
a* 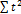 =
= 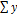 *t.
*t.
Решая систему уравнений, находим параметр b – начальную скорость роста, a – постоянную скорость изменения прироста.
Дата добавления: 2015-05-21; просмотров: 2279;
