Гравитационное разделение фаз
Практическое занятие 6
ОТСТОЙНИКИ И РЕЗЕРВУАРЫ
Технологические расчеты отстойников
Гравитационное разделение фаз
При сборе и подготовке нефти на промыслах приходится иметь дело с самыми разнообразными смесями, образующими суспензии, эмульсии, пены, туман, дым (пыль). При достаточном различии плотностей дисперсной и дисперсионной фаз наиболее простым методом их разделения является отстаивание.
В поле тяжести на оседающую (всплывающую) частицу действуют: разность силы тяжести и подъемной силы Архимеда
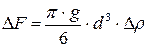, (5.1)
где Δρ – разность плотностей частицы и окружающей среды,
g – ускорение свободного падения,
d - диаметр частицы,
Сила сопротивления сплошной среды:
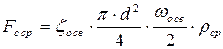, (5.2)
где ζo св – коэффициент гидравлического сопротивления сплошной
среды движению в ней одиночной частицы,
ωo св – скорость свободного движения одиночной частицы,
относительно сплошной среды,
ρср – плотность сплошной среды.
|
Допустим, что температура во всех точках аппарата гравитационного разделения (отстойника) одинакова, тогда конвекционные потоки отсутствуют. При постоянной скорости движения частицы в среде:
ΔF = Fc ср. (5.3)
Откуда, с учетом (5.1) и (5.2),следует
ζo св∙Reo св2 = 4 / 3∙Ar, (5.4)
где Reo св – критерий Рейнольдса
Reo св = ωo св∙d∙ρcр/μcр, (5.5)
где μср – динамическая вязкость сплошной среды,
Ar - критерий Архимеда:
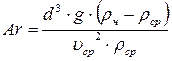, (5.6)
где υср – кинематическая вязкость сплошной среды,
ρч – плотность дисперсной фазы (частицы, капли).
В условиях стесненного осаждения (всплытия) частиц, т. е. при взаимодействии между частицами, имеем аналогично (5.4) равенство:
ζд∙Reд2 = 4 / 3∙Ar, (5.7)
где ζд – коэффициент гидравлического сопротивления для
дисперсной фазы в эмульсии,
Reд – критерий Рейнольдса в условиях стесненного потока.
Так как правые части (5.4) и (5.7) одинаковы, то:
ζд∙Reд2 = ζo∙Reo2. (5.8)
Пусть:
ζд = ζо ст∙f(W), (5.9)
где ζо ст – коэффициент гидравлического сопротивления сплошной
среды для одной частицы в условиях стесненного потока,
W – объемная доля дисперсной фазы в системе, т.е например,
обводненность эмульсии.
Экспериментальными исследованиями показано, что скорости оседания частицы в условиях свободного осаждения и стесненного потока связаны соотношением:
ωо ст = ωо св∙(1 – W)n, (5.10)
где ωо ст – скорость осаждения частицы относительно сплошной
среды в условиях стесненного потока,
ωо св – скорость свободного осаждения частицы.
Поэтому:
Reд = (1 – W)n∙Reo.св (5.11)
Экспериментально также установлено, что при Re < 500
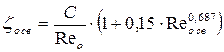, (5.12)
где:
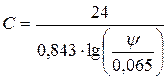, (5.13)
где ψ – коэффициент формы частицы, равный
отношению площадей поверхностей сферической частицы и
реальной частицы одинакового объема. Для сферических частиц
ψ = 1, следовательно, С = 24.
Из (5.8) и (5.9) следует:
ζо св∙Reo св2 = ζо ст∙f(W)∙Reд2. (5.14)
Откуда, с учетом (5.12), получают:
Reo св∙(1 + 0,15∙Reo св0,687) = f(α)∙Reд∙(1 + 0,15∙Reд0,687). 5.15)
При малых Re из (5.11) и (5.15) следует:
f(W) = (1 – W)-n. (5.16)
При Re > 500 коэффициент сопротивления не зависит от скорости, следовательно, ζо св = ζо ст, поэтому из (5.14):
Reo св2 = f(W)∙Reд2. (5.17)
Тогда из (5.11) и (5.17) имеем:
f(W) = (1 – W)(-2n). (5.18)
Экспериментальными исследованиями установлено, что f(W), определяемая по формулам (5.16) и (5.18), изменяется от (1 – W)(-4,65) до (1 – W)(-4,78), следовательно, в первом приближении принимают, что:
f(W) = (1 – W)(-4,7) (5.19)
Поэтому вместо (5.10) можно записать:
ωо ст / ωо св = (1 – W)4,7. (5.20)
Известны также следующие эмпирические формулы для учета влияния стесненности:
при W<0,3
ωо ст / ωо св = (1 – W)2∙10(-1,82∙W). (5.21)
при W≥0,3
ωо ст / ωо св = 0,123 / W∙(1 – W)3. (5.22)
Рассмотрим пример.
Сопоставить расчетные относительные скорости оседания капель воды в нефти в зависимости от ее обводненности, определенной по (5.20), (5.21) и (5.22)
Решение:
Пусть обводненность водонефтяной эмульсии равна 5 %, тогда по (5.20)
ωо ст / ωо св = (1 – W)4,7. (5.20)
где W - объемная доля дисперсной фазы в системе, т.е например,
обводненность эмульсии,
ωо ст - скорость осаждения частицы относительно сплошной среды
в условиях стесненного потока,
ωо св - скорость свободного осаждения частицы.
ωо ст / ωо св = (1 – 0,05)4,7 = 0,7858
Известны также следующие эмпирические формулы для учета влияния стесненности:
при W<0,3
ωо ст / ωо св = (1 – W)2∙10(-1,82∙W). (5.21)
при W≥0,3
ωо ст / ωо св = 0,123 / W∙(1 – W)3. (5.22
ωо ст / ωо св = (1- 0,05)2 ∙10(-1,82 ∙0,05) = 0,7319
Разность результатов расчетов составляет:
0,7858 – 0,7319 = 0,0539
Результаты аналогичных расчетов для других обводненностей представлены в таблице. Как следует из таблицы, сравниваемые формулы дают близкие результаты, поэтому пользоваться можно любыми из них. Надо вычислять в %, тогда можно сравнивать.
Таблица 5.1
Сопоставление результатов расчетов
| Обводненность в % | Результаты расчетов по формулам | Разность | ||
| 5.20 | 5.21 | 5.22 | ||
| 0,7858 | 0,7319 | - | 0,0539 | |
| 0,6095 | 0,5327 | - | 0,0768 | |
| 0,3504 | 0,2768 | - | 0,0736 | |
| 0,1871 | - | 0,1406 | 0,0465 | |
| 0,0906 | - | 0,0664 | 0,0242 | |
| 0,0385 | - | 0,0308 | 0,0077 | |
| 0,0135 | - | 0,0131 | 0,0004 |
Дата добавления: 2015-05-19; просмотров: 1370;