Создание учетной записи пользователя

Задача легко решается на примере 2 х ступенчатой схемы (см. рисунок)

Рис. Схема порционной экстракции при n =2.

Цель анализа в установлении такой величины d₁ при которой массообмен происходит с наибольшей полнотой (минимальном значении конечной концентрации рафината при известном значении общего расхода экстрагента.

Выше было получено выражение для второй ступени в виде

. Заменяя d₂ через D-d₁, получают

.

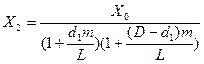Числитель последнего уравнения не зависит от d₁. Знаменатель (Zn) состоит из двух сомножителей. Согласно первому сомножителю в Zn рост d₁ вызывает уменьшение X₂, а согласно 2 му - увеличение X₂. Значит функция 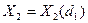может иметь экстремум. Для проверки его существования и определения d₁ в точке экстремума надо взять производную знаменателя и приравнять ее нулю

Откуда следует, что

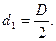
Анализ типа экстремума (приравнивание второй производной нулю) показывает, что в точке экстремума Zn проходит через максимум. Значит при 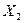минимальна.

Степень извлечения при проведении процесса порционной экстракции (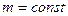 , , d₁ = d₂ = d₃ = …= d_n = d = D/n).

Если тогдаd₁ = d₂ = d₃ = …= d_n = d = D/n,тогда

.

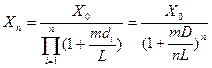Принимая, что 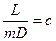, получим

, где .

Найдем предельное значение состава рафината на выходе из последней ячейки порционной экстракции при неограниченном стремлении числа ячеек к бесконечности.

, так как 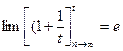- есть замечательный предел, основание натурального логарифма.

Степень извлечения при порционной экстракции может быть рассчитана по формуле

. (1)

Найдем предельное значение степени извлечения при порционной экстракции

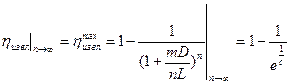, или раскрывая значение c, получим

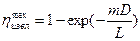. (2)

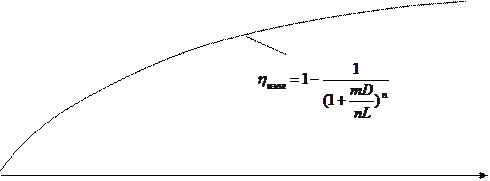Рис. Сопоставление степеней извлечения при порционной экстракции для конечного числа ступеней с максимально возможной степенью извлечении при бесконечно большом числе ступеней.

Создание учетной записи пользователя

Для создания учетной записи пользователя в Linux применяется команда useradd (обычно в каталоге /usr/sbin/, в некоторых системах именуемая adduser). Простейший способ создания учетной записи пользователя – с параметрами, устанавливаемыми по умолчанию. Например, чтобы создать учетную запись для пользователя user1, достаточно ввести

# /usr/sbin/useradd user1

По этой команде выполняется следующая последовательность операций создания учетной записи:

создание записи в файле /etc/passwd без указания пароля. В некоторых версиях Linux пользователь не может воспользоваться своей учетной записью, пока не определен пароль;

присвоение пользователю идентификатора. В Linux в качестве идентификатора пользователя по умолчанию выбирается минимальное число, которое больше 500 и больше идентификаторов всех существующих пользователей;

включение пользователя в определенную группу. В Linux это означает создание группы, в которую будет включен один конкретный пользователь;

создание исходного каталога для данного пользователя (в большинстве систем Linux - каталог /home/user1) и копирование в него содержимого скелетного каталога /etc/skel.

При создании учетной записи по команде useradd задача предоставления пароля пользователю остается за администратором системы.

Для указания идентификатора пользователя непосредственно в команде useradd создания учетной записи служит флажок –u:

# useradd -и 10001 user1

По этой команде создается учетная запись пользователя user1 с идентификационным номером 10001.

Для добавления нового пользователя в группу (например, users) используется флажок -g.

# useradd -g users user1

Чтобы определить пользователю другой исходный каталог, нужно указать в команде флажок -d.