Зависимости для идеального газа

Под идеальным понимается такой газ, у которого объем, занимаемый молекулами газа, пренебрежительно мал по сравнению с заполняемым им объемом и отсутствуют силы взаимного притяжения. Для идеального газа справедливы законы, определяющие взаимную связь основных термодинамических параметров его состояния по уравнению (2.1).

Зная два параметра состояния, например V и Т, можно найти третий параметр – р.

Закон Бойля–Мариотта для процесса при постоянной температуре (Т = const) записывается в виде выражения

p₁V₁ = p₂V₂= const.(2.2)

Закон Гей-Люссака для процесса при постоянном давлении (р = const) выглядит следующим образом:

V = V₀ (1 + α_pt) и V/T = const, (2.3)

здесь a_p = 1/273,16 – средний коэффициент термического расширения при р = const.

Характеристическое уравнение Клапейрона–Менделеева имеет вид

pV = GRT,(2.4)

для 1 кг рυ = RT,

Закон Авогадро гласит, что в равных объемах идеальных газов при одинаковых давлении и температуре содержится одинаковое число молекул:

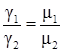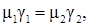или (2.7)

где 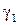, – удельный вес газов.

Уравнение Клапейрона–Клаузиуса характеризует изменения равновесного давления (по кривой фазового равновесия) в зависимости от температуры:

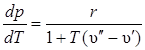, (2.10)

где r – удельная теплота фазового перехода; – удельный объем насыщенной жидкости; – удельный объем сухого насыщенного пара.

Зависимости для газовых смесей соответствуют характеристическому уравнению.

Закон Дальтона для газовой смеси определяет связь между давлением смеси р_см и парциальными давлениями р_i отдельных компонентов в смеси газа:

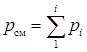. (2.11)