Откачка паров кипящей жидкости.

Процесс в жидкости при уменьшении давления над ее зеркалом в изолированном сосуде напоминает процесс кипения. Через слой жидкости поднимаются пузырьки пара, который откачивается вакуумным насосом. Однако при откачке могут существовать режимы только поверхностного испарения. Во всех случаях испаряющийся пар отнимает энергию у жидкости и внутренних стенок сосуда, вследствие чего температура остающейся жидкости и стенок снижается. Пусть r – скрытая теплота испарения жидкости; m – масса жидкости в сосуде; m_cт – масса внутренних стенок; с_ж и с_ст – теплоемкость жидкости и материала стенок; Q_c – теплоприток через изоляцию. Уравнение баланса энергии в элементарном квазиравновесном процессе в предположении равенства температур жидкости и стенок запишем следующим образом:

rdm=(m–dm)c_жdТ+m_стс_стdТ+dQ_c.

Скорость изменения температуры жидкости в сосуде определенной геометрии определяется в основном интенсивностью откачки ее паров, т.е. производительностью вакуумного насоса. При давлении p и постоянной температуре T_ВН на всасывании для массы паров dm, откачиваемых насосом, можно записать

,

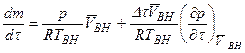где 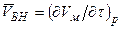– объемная производительность насоса при условиях всасывания (для машин объемного типа – описанный объем в единицу времени); ∆τ – продолжительность работы насоса. Следует учитывать, что производная 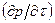отрицательна.

Разные криогенные жидкости имеют различные зависимости р=f(Т); с_ж=f(Т), поэтому при использовании одинаковых насосов темп охлаждения, при прочих одинаковых условиях, разный. Прекращение охлаждения (равновесие) происходит при понижении давления до такой величины, при которой уменьшение энергии компенсируется внешним теплопритоком.

Используя усредненные параметры, легко вывести упрощенные соотношения в интегральной форме, не учитывая динамические характеристики процесса откачки. Пусть ∆m – масса испарившейся при откачке жидкости; r_ср – средняя теплота испарения жидкости; с_ж.ср и с_ст.ср – средние теплоемкости жидкости и стенок. Тогда можно записать

r_ср∆m≈(m_н–∆m)с_ж.ср∆Τ+0,5mс_ж.ср∆Τ+m_стc_ст.cp∆Τ+Q_c,

где m_н – начальная масса жидкости.

Разделив это уравнение на m_н и обозначив относительные массы и теплопритоки 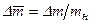; ; 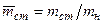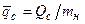, найдем в первом приближении снижение температуры жидкости при откачке ее доли ∆m:

.

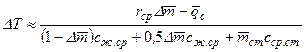На практике этот метод часто применяют для получения недогретых (переохлажденными) жидкостей.