Модель количественной олигополии Курно

Модели количественной олигополии более адекватны в ситу ации, когда фирмам после принятия плана трудно изменить производственные мощности, а следовательно, и объем поставок. Это характерно для отраслей тяжелой промышленности, машиностроения, нефте- и газодобычи и т.д. Основными количественными моделями являются модель Курно, модель Штакельбсрга и модель ломаной кривой спроса. В соответствии с целями учебного пособия мы рассмотрим только модель Курно.

Модель Курно основывается на следующих предпосылках:

· на рынке присутствуют только две фирмы (дуополия);

2) каждая фирма, принимая свое решение, считает цену и объем производства конкурента постоянными.

Допустим, что фирмы схожи как по размерам, так и по уровню своих издержек (для простоты примем постоянные издержки равными нулю, FС₁=FС₂=0). Рыночный спрос известен и имеет вид линейной функции,

р = a - bQ. (1)

Совокупный объем производства двух фирм Q=Q₁+Q₂. Издержки фирм пропорциональны объему производства:

TC_i(q_i)=c_iq_i.(2)

Здесь величину a можно интерпретировать как максимальную цену - цену, при которой последний покупатель уходит с рынка. Коэффициент b показывает, насколько нужно снизить цену, чтобы увеличить продажи на единицу, а c_i характеризует предельные издержки (издержки производства дополнительной единицы продукции) i-фирмы MC_i(q_i) = TC'_i(q_i) = c_i = const.

Каждая фирма стремится к максимизации прибыли, исходя из неизменности объема выпуска конкурента, независимо от того какой объем выберет она сама. Таким образом, оптимальный объем производства фирмы l будет меняться в зависимости от того, как, по ее мнению, будет расти объем выпуска фирмы 2. Уравнения кривых реакции имеют следующий вид:

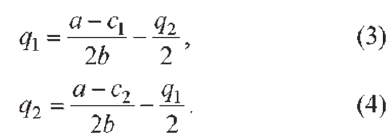
Кривые реагирования - это множества точек наивысшей прибыли, которую может получить один из дуополистов при данной величине выпуска другого. Множества этих точек называют кривыми реагирования, поскольку они указывают на то, как один из дуополистов, выбирая величину своего выпуска, q_l, будет реагировать на решение другого дуополиста относительно величины своего выпуска, q₁(i ≠ j).

Точка пересечения кривых реагирования обоих дуополистов, совмещенных в одном двухмерном пространстве выпусков, определяет равновесие Курно¹¹⁰. Равновесие в дуополии Курно (1), (2) определяется в результате решения системы линейных уравнений (3), (4) и имеет вид

(5)

Равновесие в дуополии Курно - это точка, в которой каждая из фирм максимизирует свою прибыль с учетом данного выпуска конкурирующей фирмы. Такое поведение фирмы является наилучшим ответом на известное поведение соперника. Ни у одной из фирм нет побудительных мотивов менять свою реакцию на поведение соперника. Такое равновесие, частный случай которого проанализирован в модели Курно, получило название равновесие Нэша по имени американского экономиста Дж.Ф. Нэша (лауреат Нобелевской премии по экономике 1994 г. за развитие теории игр)¹¹¹. Равновесие, по Нэшу, - это точка, в которой ни одному из олигополистов невыгодно в одностороннем порядке менять параметры равновесия.

Графически эта ситуация для случая одинаковых (с₁=с₂=с, рис. 60а) и различных (с₂ <с₁ рис. 60б) издержек производства. Точка пересечения кривых реакции обоих фирм, совмещенных на единых координатных осях, показывает равновесные объемы выпуска в условиях некооперируемои олигополии и называется точкой равновесия Курно. В точке равновесия ни фирма 1, ни ее конкурент не заинтересованы в увеличении объемов выпуска в одностороннем порядке.

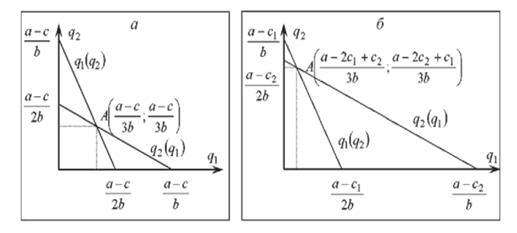
Рис. 60. Кривые реакции в модели Курно. Случаи одинаковых (а) и различных (б) издержек производства

В случае равных издержек производства формулы (5) упрощаются, принимая вид

(6)

В случае же, когда издержки одной из фирм (допустим, второй) уменьшаются, она завоевывает большую долю рынка. А если выполняются следующие равносильные неравенства

(7)

то первая, т.е. более дорогая, фирма добровольно уходит с рынка, вторая поставляет продукцию в объеме q₂=(a – с₂ )/2b .