Многокаскадные усилители с RC- связями

8.11.1. Основные свойства, эквивалентные схемы

Резисторный каскад является основ­ным типом каскада предварительного усиления ввиду простоты, дешевизны, малых размеров и очень хороших частотной, фазо­вой и переходной характеристик.

В резисторном каскаде предварительного усиления может быть использован любой усилительный элемент малой мощности, дающий достаточное усиление, − чаще всего биполярный или полевой транзистор, реже всего − диод с отрицательным сопротивлением.

Биполярные транзисторы в резисторных каскадах предварительного уси­ления обычно включают с общим эмиттером, так как только при этом можно соединить последовательно несколько каскадов, по­лучая от каждого из них высокое усиление сигнала. Включение с общей базой целесообразно лишь для входных каскадов, работающих от источника сигнала с малым внутренним сопротивлением и в случае необходимости расширения полосы усиления – в область верхних частот. Включение с общим коллектором (эмиттерный повтори­тель) применяется в тех случаях, когда источник сигнала высокоомный или же каскад работает на низкоомную нагрузку. Полевые транзисторы обеспечивают еще более высокое входное сопротивление, чем эмиттерный повторитель. Типовая принципиальная схема резисторного каскада приведена на рис. 8.55.

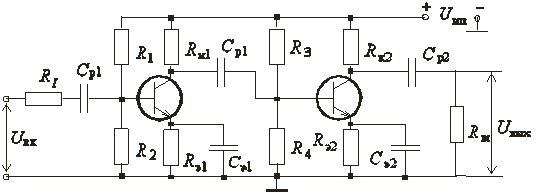
Рис. 8.55

Для упрощения анализа её свойств предположим, что емкость конденсаторов С_ри С_эочень вели­ка, тогда их сопротивлением для частот сигнала можно пренебречь. Полагая, что на вход каскада подается установившееся синусоидальное напряжение 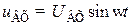, заменим выходную цепь первого усилительного каскада генератором напряжения с ЭДС μ 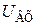с внутренним сопротивле­нием 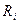. Подключив к генера­тору сопротивление R_ки па­раллельно ему последователь­ную цепочку 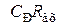, так же как на принципиальной схеме,по­лучим эквивалентную схему резисторного каскада (сплошные ли­нии на рис. 8.56).

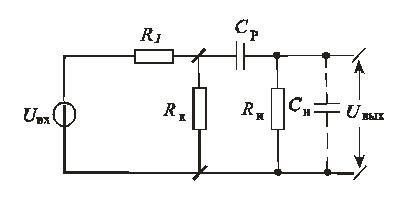
Рис. 8.56

Исследования показали, что такая схема справедлива лишь для частот не выше нескольких килогерц; чтобы сделать её при­годной для более высоких частот, необходимо учесть емкости, отсутствующие в принципиальной схеме, а именно выходную ёмкость усилительного элемента C_вых, ёмкость монтажа С_ми ёмкость нагрузки 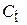. Без заметной погрешности можно считать эти ёмкости включенными между выходными зажимами схемы и заменить их ёмкостью .

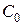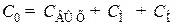. (8.170)

Увеличение сопротивления разделительного конденсатора С_рс понижением частоты вызывает увеличение на нём падения на­пряжения сигнала, вследствие чего выходное напряжение с понижением частоты падает.

Уменьшение сопротивления ём­кости С₀ с повышением частоты приводит к снижению напряжения сигнала на ней, являющегося выходным напряжением каскада.

Таким образом, коэффициент усиления резисторного каскада падает на нижних частотах из-за воз­растания сопротивления разделительного конденсатораи на верх­них частотах из-за уменьшения со­противления ёмкости С₀ (рис. 8.57) и частотных свойств транзисторов.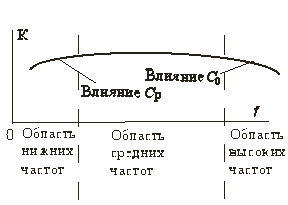

Рис. 8.57

Поэтому область частот на горизонтальной оси графика (рис. 8.57) можно разделить на три части: область нижних частот, в которой ска­зывается влияние разделительного конденсатора, область верхних частот, где влияет ёмкость С₀, и область средних частот, где практически отсутствует влияние как С_р, так и С₀.

На основании этого для облегчения анализа частотной и фа­зовой характеристик из полной эквивалентной схемы рис. 8.56 можно составить три частные эквивалентные схемы: схему для нижнихчастот, в которой отсутствует ёмкость С₀, не влияющая в этой области частот; схему для средних частот, где ёмкость С₀ отсутствует, а ёмкость С_рзакорочена, так как ни та, ни другая в этой области частот не влияют; и схему для верхних частот, где закорочена ёмкость С_р, так как её сопротивление в этой области частот ничтожно мало.

При подаче на вход резисторного каскада мгновенного скач­ка напряжения ёмкости С₀ и С_рначинают заряжаться. Малая по величине ёмкость С₀, заряжающаяся от параллельно соеди­нённых сопротивлений R_i, R_к, R_н , заряжается быстро. Так как напряжение на ёмкости С₀ представляет собой выходное напря­жение каскада, последнее достигает установившегося значения через очень малый промежуток времени. За это время раздели­тельный конденсатор С_рбольшой ёмкости, заряжающийся через сопротивление R_н, не успевает заметно зарядиться и на­пряжение на нём в процессе заряда ёмкости С₀ можно считать равным нулю. Это позволяет закоротить конденсатор С_р, исклю­чив тем самым его из схемы при определении времени установления каскада; эквивалентная схема при этом упрощается, при­нимая вид схемы для верхних частот.

Поэтому нахождение переходной характеристики в области малых времен, определяющей время установления каскада, ведётся по эквивалентной схеме для верхнихчастот.

Процесс заряда конденсатора С_р через сопротивление R_н занимает много больше времени, чем заряд ёмкости С₀; поэтому при рассмотрении процесса заряда С_р ёмкость С₀ можно считать уже заряженной и отключить от схемы, после чего эквивалент­ная схема каскада примет вид схемы для нижних частот. Так как выходное напряжение U_выхпредставляет собой разность напряжения на выходе усилительного элемента и напряжения на разделительном конденсаторе, по мере заряда конденсатора С_рвыходное напряжение будет падать, вызывая тем самым спад вершины усиливаемых импульсов.

Поэтому нахождение переходной характеристики в области больших времён, определяющей искажения вершины усиленных импульсов, ведётся по эквивалентной схеме для нижних частот.

Из сказанного можно заключить, что:

1) частотная и фазовая характеристики в области нижних частот определяют переходную характеристику в области больших времён, а следовательно, и искажения вершины усиленных импульсов;

2)частотная и фазовая характеристики в области верхних частот определяют переходную характеристику в области ма­лых времён, а следовательно, время установления и выброс.

8.11.2. Область нижних частот

Для упрощения эквивалентной схемы, изображённой на рис.(рис. 8.58, а), заменим в ней генератор с ЭДС и внутренним со­противлением R_i, шунтированный сопротивлением R_К, эквивалентным генератором. Это устранит в схеме параллельную ветвь; внутреннее сопротивление эквивалентного генератора для ниж­них частот R_эн и его ЭДС U_эннайдём методом холостого хода и короткого замыкания, применяемым в электротехнике.

Эквивалентный генератор при отсутствии нагрузки (холостом ходе) должен иметь на выходе напряжение :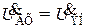

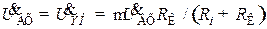. (8.171)

Ток короткого замыкания эквивалентного генератора 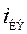должен быть равен току короткого замыкания схемы

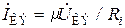. (8.172)

Внутреннее сопротивление эквивалентного генератора определится как отношение его ЭДС к току короткого замыкания

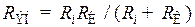. (8.173)

Следовательно, сопротивление эквивалентного генератора равно сопротивлению параллельного соединения сопротивления, шунтируемого генератора и шунтирующегосопротивления.

Заменив шунтированный генератор эквивалентным с параметрами, определяемыми уравнениями (8.172) и (8.173), получим упрощённую эквивалентную схему резисторного каска­да для нижних частот, изображённую на рис.8.58.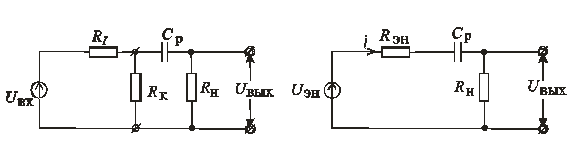

а б

Рис. 8.58

Из неё сле­дует, что выходное напряжение резисторного каскада в области нижних частот равно произведению тока в цепи I на сопротивление 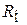. Ток I равен ЭДС μ 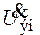, делённой на полное

сопротивление цепи, т.е.

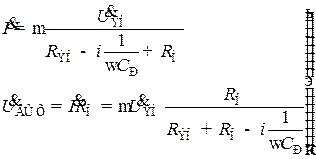. (8.174)

На средних частотах последнее слагаемое знаменателя полученных выражений пренебрежимо мало по сравнению с суммой первых двух, а следовательно, выходное напряжение на средних частотах определится так:

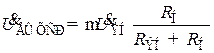. (8.175)

Поделив (U_вых на U_{вых ср}), получим относительное усиление в комплексной форме для резисторного каскада в области нижних частот: 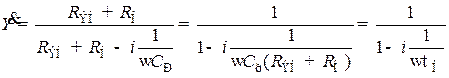, (8.176)

где 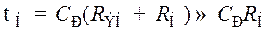(8.177)

имеет размерность времени и называется постоянной времени нижних частот резисторного каскада. Аргумент выражения (8.176) есть угол сдвига фазы 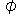выходного напряжения относительно входного в области нижних частот. Этот угол определится как арктангенс отношения мнимой части выражения (8.176) к действительной: 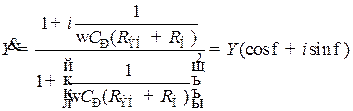(8.178)

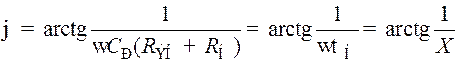, (8.179)

где X – нормированная частота для области нижних частот, равная

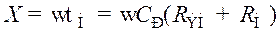. (8.180)

Из (8.179) видно, что при изменении частоты сигнала от 0 до , тангенс угла сдвига фазы меняется от 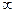до 0. Отсюда следует, что угол сдвига фазы между выходным и входным на­пряжениями резисторного каскада в области нижних частот стре­мится к +90°, при безграничном понижении частоты, и к 0° на средних частотах, где X становится очень большим. Положи­тельное значение 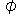показывает, что в области нижних частот выходное напряжение опережает по фазе входное.

Из рис. 8.58, б видно, что при частоте, стремящейся к нулю, сопротивление цепи стремится к бесконечности и становится ёмкостным. При этом ток I в цепи опережает ЭДС Ů_вх,а следовательно, и входное напряжение Ů_вх на 90°. Так как выходное напряжение Ů_вхравно IR_н –в фазе с током, то и выходное напряжение при частоте, стремящейся к нулю, опережает входное на 90°.

При 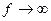сопротивление конденсатора Срничтожно мало и сопро­тивление цепи практически активно; поэтому ток в цепи, а следовательно, и выходное напряжение будут в фазе с входным напряжением.

Модуль относительного усиления, определяющий вносимые резисторным каскадом частотные искажения и его частотную характеристику на нижних частотах, получим из (8.178): 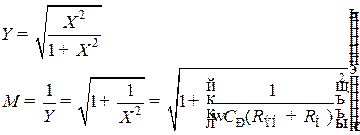. (8.181)

Из (8.181) видно, что при безграничном понижении частоты относительное усиление, а следовательно, и коэффициент уси­ления резисторного каскада стремятся к нулю; при повышении частоты Y стремится к единице, а К − к усилению на средних частотах.

Действительно, из рис. 8.58 видно, что при безграничном понижении ча­стоты сопротивление конденсатора Срстремится к бесконечности, ток в цепи стремится к нулю, а следовательно, и выходное напряжение также стремится к нулю. При возрастании частоты сопротивление конденсатора С_р стремится к нулю, а выходное напряжение − к своему значению на средних частотах.

Положив в формуле (8.181) 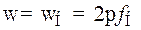и решив её относительно Ср, получим выражение, определяющее необходимую ёмкость разделительного конденсатора по заданному коэффициенту ча­стотных искажений М_нот влияния этого конденсатора на низ­шей рабочей частоте f_н:

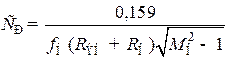. (8.182)

Для определения переходной характеристики резисторного каскада в области больших времён заменим в (8.181) Y на f(p) и 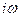на оператор p, после чего получим

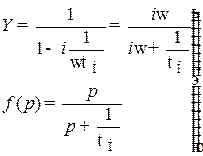. (8.183)

Из таблиц найдём оригинал, соответствующий изображению (8.183) и представляющий собой нормированную переходную характеристику резисторного каскада в области больших времён:

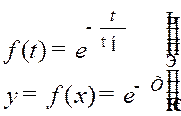, (8.184)

где Х, представляющий собой нормированное время, равен

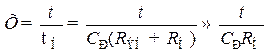. (8.185)

Отсюда, согласно (8.184, (8.185), спад 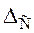вершины импульса длительностью T, вызванный влиянием разделительного конденсатора, составит

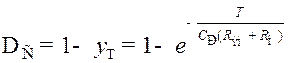. (8.186)

Решая (8.186) относительно Ср, получим формулу для определения необходимой ёмкости разделительного конденсатора, по допустимой величине спада 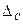и длительности импульса T:

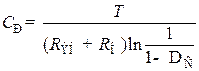. (8.187)

При 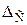<<1, что обычно имеет место, 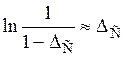, в чем нетрудно убедиться разложением в ряд Тейлора. Выражения для Ср упрощается

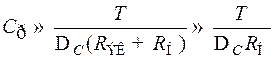, (8.188)

так как 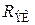<< 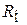. Решив (8.188) относительно 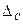, получим простую формулу

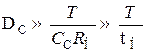, (8.189)

из которой следует, что спад численно равен отношению длительности импульса к постоянной времени каскада в области нижних частот. Так, например, для получения спада, равного 0,1 при длительности импульса 0,01 секунды, необходима постоянная времени каскада в области нижних частот, в 10 раз превышающая длительность импульса и, следовательно, равная 0,1 секунды.

8.11.3. Область средних частот

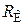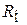С целью упрощения эквивалентной схемы (рис. 8.59, а) для средних частот заменим параллельно включённые и сопротивлением 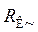, равным 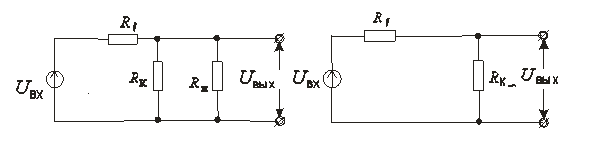а б Рис. 8.59

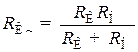. (8.190)

Здесь 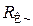представляет собой сопротивление нагрузки выходной цепи усилительного элемента переменному току.

После этой замены эквивалентная схема резисторного каска­да для средних частот примет вид, изображенный на рис. 8.59, б.

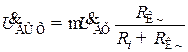. (8.191) Расчётный коэффициент усиления каскада считают равным отношению выходного напряжения на средних частотах к вход­ному напряжению; поэтому расчётный коэффициент усиления резисторного каскада 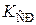найдём, поделив (8.191) на U_вх:

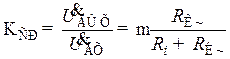. (8.192)

Заменим в в выражении (8.192) 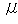на 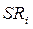, после чего получим

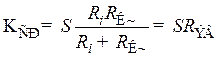, (8.193)

где 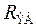− сопротивление эквивалентного генератора на верхних частотах, используемое далее.

Для каскадов на биполярных транзисторах удобнее пользоваться параметрами четырехполюсника, которые связаны с его крутизной

.

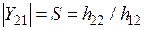Так как эквивалентная схема для средних частот содержит только активные сопротивления, частотные искажения и фазо­вые сдвиги на средних частотах практически отсутствуют.

8.11.4. Область верхних частот

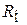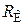Для упрощения эквивалентной схемы резисторного каскада для верхних частот, приведённой на рис.8. 60, а, заменим и на 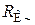), а затем приведём генератор с ЭДС 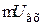и внутренним сопротивлением 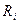,шунтированный сопротивлением 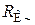,к эквивалентному генератору.

После этого эквивалентная схема примет вид, изображённый на рис. 8. 60, б.

а б

Рис. 8.60

ЭДС эквивалентного генератора для верхних частот 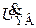и его внутреннее сопротивление 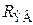определятся выражениями:

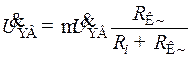, (8.194)

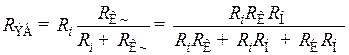. (8.195)

Находя выходное напряжение схемы рис. 8.60, б как произве­дение тока в цепи на сопротивление ёмкости С₀, получим

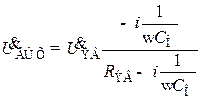. (8.196)

Преобразуя, получим

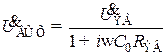. (8.197)

На средних частотах второй член знаменателя полученного выражения становится пренебрежимо мал по сравнению с еди­ницей, а следовательно, выходное напряжение на средних ча­стотах

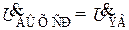. (8.198)

Поделив (8.197) на 8.198), получим относительное усиление резисторного каскада на верхних частотах в комплексной форме:

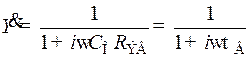, (8.199)

где 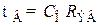имеет размерность времени и называется постоянной времени верхних частот резисторного каскада. Аргумент выражения (8.199) есть угол сдвига фазы 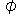выходного напряжения относительно входного в области верхних частот и определяется как арктангенс отношения мнимой части (8.199) к действительной:

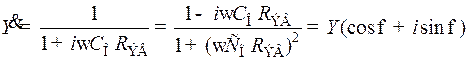; (8.200) 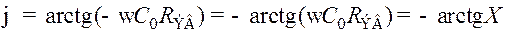, (8.201)

где X — нормированная частота для области верхних частот, равная

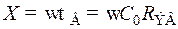. (8.202)

Из (8.201) следует, что угол сдвига фазы между выходным и входным напряжениями резисторного каскада в области верхних частот стремится к 90° при безграничном повышении часто­ты, и к 0° на средних частотах, где X становится ничтожно ма­лой величиной. Отрицательное значение 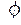показывает, что в области верх­них частот выходное напряжение отстаёт по фазе от входного.

Сказанное видно и из эквивалентной схемы рис. 8.60, б. При безграничном повышении частоты сопротивление ёмкости С₀ становится ничтожно малым и ток сигнала в цепи оказывается в фазе с 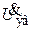, а, следовательно, и с 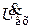. Так как 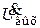снимается с ёмкости С₀, то оно будет отставать от тока, а значит, и от входного напряжения на 90°. При малых значениях 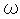сопротивление цепи практически чисто ёмкостное и ток в цепи опережает ЭДС на 90°, а так как выходное напряжение отстаёт от тока на 90°, оно оказывается в фазе с входным.

Модуль относительного усиления, определяющий вносимые резисторным каскадом частотные искажения и его частотную характеристику на верхних частотах, найдём из (8.201):

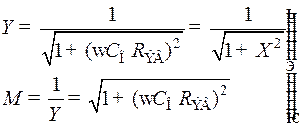. (8.203)

При возрастании частоты 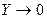, а при её уменьшении 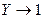. Поэтому коэффициент усиления резисторного каскада при повышении частоты падает, стремясь к нулю на очень высоких частотах, и принимает значение, рав­ное коэффициенту усиления на средних частотах при понижении частоты.

Стремление коэффициента усиления к нулю при повышении частоты обусловлено тем, что сопротивление ёмкости С₀, с которой снимается выходное напряжение, при этом также стремится к нулю.

Приравняв 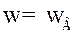, М = М_ви решив (8.203) относительно 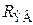, получим

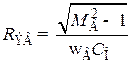. (8.204)

Чтобы коэффициент частот­ных искажений рассчитываемого каскада на высшей рабочей ча­стоте не превысил заданной величины М_в, необходимо 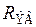иметь равным или меньше найденного из (8.204). 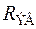представляет собой сопротивление параллельно сое­динённых R_i, R_ви R_к; его уменьшение возможно за счёт уменьшения любого из этих трёх сопротивлений.

Для определения переходной характеристики резисторного каскада в области малых времён заменим в (8.201) У на f(p) и 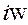на оператор p, что даст

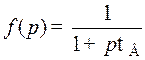. (8.205)

Из таблиц решений операторных уравнений найдём оригинал, соответствующий изображению (8.205) и пред­ставляющий собой нормированную переходную характеристику резисторного каскада в области малых времён

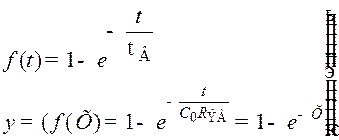(8.206)

где Х – нормированное время, равное

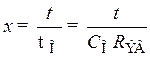. (8.207)

Время установления резисторного каскада 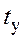нетрудно найти по уравнению переходной характеристики в области малых времён, определив из него 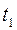, соответствующее Y = 0,1, и t₂, соответствующее Y = 0,9:

; ;

; .

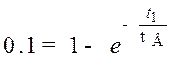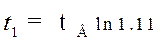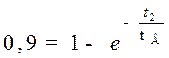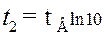Отсюда 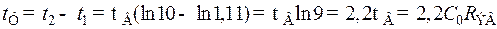, (8.208)

и нормированное время установления резисторного каскада

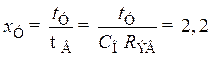. (8.209)

Расчётную формулу для определения сопротивле­ния в коллекторной цепи резисторного каскада по заданному времени установления получим из (8.208):

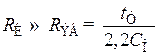. (8.210)

Найдём соотношения, связывающие переходные искажения с частотными и фазовыми искажениями резисторного каскада. Определим частотные и фазовые искажения, вносимые каскадом при синусоидальном сигнале с длительностью полупериода, рав­ной длительности импульса Т. Частота такого сигнала f связана с T соотношением

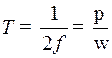. (8.211)

Для определения связи времени установления резисторного каскада t_y с его верхней граничной частотой 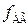(частотой, на которой относительное усиление Y_вг= 0,707) положим в (8.203) 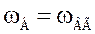; 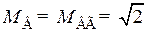. Решим полученный результат относительно С₀R_вги подставим найденное значение в (8.210). Это даст:

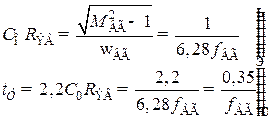. (8.212)

Следовательно, каскад с верхней граничной частотой 10 МГцбудет иметь время установления 0,035 мкс = 35нс.

Полученные соотношения для каскадов с коррекцией, а также для многокаскадных усилителей являются приближёнными.

8.12. УСИЛИТЕЛИ ПОСТОЯННОГО ТОКА

УПТ, или усилителями медленно изменяющихся токов и напряжений называют усилители, коэффициент усиления которых при уменьшении частоты сигнала до 0 остается таким же, как и на средних частотах, т.е. не равен 0. Их низшая рабочая частота f_н = 0, а высшая рабочая частота f_в определяется назначением усилителя. Амплитудная и частотная характеристики имеют следующий вид (рис. 8.61, 8.62):

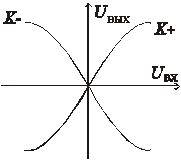
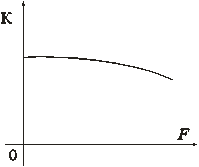
Рис. 8.61 Рис. 8.62

УПТ используют в вольтметрах, осциллографах, схемах автоматической регулировки усиления, в приемниках, стабилизаторах тока и напряжения, в приборах для измерения неэлектрических величин, в управляющих и следящих системах и многих других устройствах.

По принципу действия УПТ делят на:

1) УПТ прямого усиления;

2) УПТ с преобразованием.

8.12.1. УПТ прямого усиления

Для УПТ пригодными являются только гальванические межкаскадные связи, т.е. связи не зависящие от частоты. При разработке УПТ необходимо решать следующие основные проблемы: согласование потенциальных уровней в различных частях схемы и уменьшение нестабильности. Остановимся на вопросах связи каскада с источником сигнала и нагрузкой. Варианты согласования потенциальных уровней приведены на рис. 8.63, 8.64.

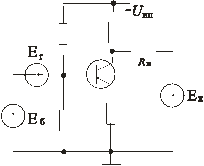
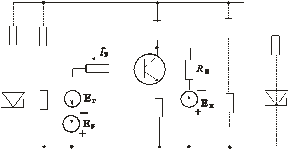Рис. 8.63 Рис. 8.64

Однако УПТ подвергнуты дрейфу нулевого уровня (нуля). Это обусловлено изменением напряжения питания, изменением температуры, изменением с течением времени параметров схемы.

Для уменьшения дрейфа нулямогут быть применены следующие методы:

1) применение глубокой отрицательной обратной связи;

2) компенсация температурного дрейфа элементами с нелинейной зависимостью параметров от температуры;

3) применение балансных (мостовых) схем;

4) преобразование постоянного тока в переменный и усиление переменного тока с последующим выпрямлением (усиление с модуляцией и демодуляцией);

5) применение дополнительного усилителя в цепи автоматицеской стабилизации нулевого уровня.

Применение глубокой отрицательной обратной связи полностью не устраняет дрейфа нуля и не улучшает отношение сигнала к дрейфу. Для увеличения усиления в УПТ, охваченном обратной связью, целесообразно применять каскады, построенные с чередованием транзисторов p-n-p и n-p-n. Частичная компенсация дрейфа нуля, обусловленного токами I_К0, происходит в многокаскадных УПТ с четным количеством каскадов. Действительно, положительное приращение обратного тока коллектора первого каскада ΔI_К01 вызывает отрицательное изменение тока ΔI_К2. Приращения ΔI_К2 и ΔI₀₂ имеют различные знаки.

Применение балансных схем является более надежным методом уменьшения дрейфа нуля. Балансные каскады в сочетании со взаимной компенсацией, глубокой отрицательной обратной связью и термокомпенсацией нелинейными элементами дают возможность существенно увеличить стабильность УПТ (рис.8.65, а, б). Схема параллельного балансного типа приведена на рис. 8.65, а.

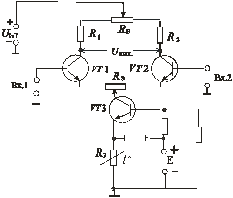
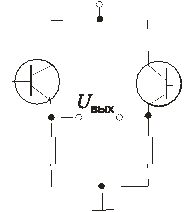
а б

Рис. 8.65

Иногда параллельно-балансные каскады имеют эмиттерный выход (см. рис. 8.65, б), что дает возможность уменьшить выходное сопротивление схемы.

В некоторых случаях для транзисторных пар результирующий дрейф балансных каскадов линейно зависим от температуры. При этом температурную компенсацию можно построить на транзисторе, включенном в эмиттеры усилительных транзисторов, содержащий терморезистор в цепи эмиттера (см. рис. 8.65, а).

Сопротивлением R_Б производится регулировка нуля в отсутствии входного сигнала.

С помощью сопротивления R_Э можно добиться практически одинаковых изменений токов коллекторов VT1 и VT2 (приведенный ко входу дрейф может быть порядка 10 мкВ/град.). Балансные каскады могут работать и с несимметричным входом, когда сигнал подается, например, между базой первого транзистора и землей. При несимметричном входе в базу второго транзистора необходимо включать сопротивления равные R_Г.

Схема параллельно-балансного УПТ позволяет уменьшить дрейф нуля примерно на порядок.