Перехода
Зависимость тока через p-n- переход от величины приложенного напряжения называется его вольтамперной характеристикой. При расчете вольтамперной характеристики предполагают, что электрическое поле вне обедненного слоя отсутствует, т.е. все напряжение приложено к нему. Общий ток в p-n- переходе определяется четырьмя членами:
J = JPдиф – JPдр + Jnдиф – Jnдp
где
Jnдиф = qpn vpдиф = qvpдиф pn0exp(qUВН/kT)
JPдp = qpn0vpдp ; Jnдиф = qnPvnдиф = qvnдифnP0 exp(qUВН/kT); (1.18)
Jnдp = qnP0 vnдp
При небольших отклонениях от условий равновесия скорость диффузии носителей допускается близкой к их скорости дрейфа в слабом электрическом поле, во всяком случае для условий равновесия выполнимы следующие равенства:
vpдиф = vpдp = vp ; vnдиф = vn дp = vn .
Тогда соотношение (1.18) принимает вид
J = qvp [ pn0 exp(qUВН/kT) – pn0 ] +qvn [nP0 exp(qUВН/kT) – nP0]=
= qvp pn0 [exp(qUВН/kT) –1] + qvn nP0 [exp(qUВН/kT) –1] =
= q(vp + vn nP0)[exp(qUВН/kT) –1] = J0 [exp (qUВН /kT) –1] (1.19)
Таким образом, уравнение теоретической ВАХ p-n-перехода имеет вид
I = I0[exp (qUВН /kT) –1] (1.19а)
Определяя скорость носителей как vp,n = Dp,n /Lp,n, где Dp,n – коэффициент диффузии дырок или электронов, Lp,n – диффузионная длина дырок или электронов, ток насыщения или обратный ток J0 записывают:
J0 = qpn0 Dp / Lp+ qnP0 Dn / Ln (1.20)
Как известно, величины Dp, Dn , pn0, nP0, Lp=(τpDp)1/2, Ln = (τn Dn)1/2 имеют сильную зависимость от температуры, поэтому J0 называют еще тепловым током, τp,τn – время жизни неравновесных носителей заряда.
Для прямого напряжения можно пренебречь единицей по сравнению с экспоненциальной составляющей:
Jпрям ≈ J0 exp(qUВН/kT).
При обратном напряжении порядка (0,1– 0,2)В экспоненциальный член в (1.19) намного меньше единицы, и им можно пренебречь. Тогда
Jобр ≈ – J0
Рассмотрение работы p-n- перехода при воздействии внешнего напряжения показывает, что он обладает несимметричной проводимостью: в прямом направлении проводимость значительно больше, чем в обратном. Это явление находит широкое применение в полупроводниковой электронике и оценивается коэффициентом выпрямления:
Квыпр = Jпрям / Jобр ≈ exp(qUпр/kT).
Для T = 300º С kT/q ≈ 26 мВ, поэтому даже при небольшом прямом напряжении Квыпр ≈1017. Практически Квыпр ≈ 1014 . Обусловлено это тем, что прямой ток реального диода намного меньше теоретического, а обратный значительно больше теоретического. Коэффициент выпрямления в сильной степени зависит также от величины обратного напряжения.
Причинами отличия реальной характеристики от теоретической (1.19) являются:
– рекомбинация носителей заряда в обеднённом слое при их инжекции;
– влияние заряда инжектированных носителей и электрического поля, создаваемого этим зарядом, которое противоположно напряжённости отпирающего электрического поля;
– влияние падения напряжения на сопротивление толщи областей полупроводника 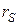 , примыкающей к обедненному слою и на контактах. Падение напряжения на этом сопротивлении Ur = IrS.
, примыкающей к обедненному слою и на контактах. Падение напряжения на этом сопротивлении Ur = IrS.
–термическая генерация носителей в обедненном слое;
– поверхностная проводимость p-n- перехода.
Поэтому уравнение вольтамперной характеристики реального перехода принимает вид:
J = J0 [exp((Uпр– IrS) / kT)–1], (1.21)
или I = JS = I0 [exp((Uпр– IrS) / kT)–1]. (1.21а)
Теоретическая и реальная характеристики представлены на рис. 1.8.
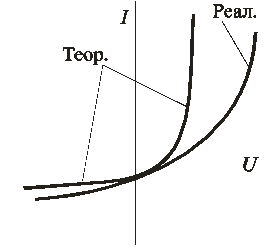
Рис. 1.8
1.4. Толщина p-n- перехода
Обедненный слой, как показано на рис. 1.5 – 1.7, имеет ширину, определяемую координатами : –XP, Xn.
L= XP + Xn .
Для идеального p-n- перехода можно записать уравнение Пуассона:
εε0 (dE/dx) = q (p – n + N(x)) (1.22)
Данное выражение разбивается на два уравнения – для левой и правой части p-n- перехода:
E(x) = dφ / dx = qNa / εε0 (X + XP) при –XP < X < 0 (1.23)
E(x) = – dφ / dx = qNd / εε0 (X + X n) при 0 < X < Xn (1.24)
Объемные заряды согласно условию непрерывности поля, слева и справа от границы p-n- перехода должны быть равны между собой:
Q = SqNa XP = SqNd Xn
где S – площадь p-n- перехода.
Проведя интегрирование выражений для E(x), получим:
(qNa / 2 εε0) XP2 + (qNd / 2 εε0) Xn2 = φK ± U (1.25)
Используя последние уравнения, находим:
XP = {2 εε0 Nd (φK ± U) / [qNa(Na + Nd)]}1/2, (1.26)
Xn = {2 εε0 Na (φK ± U) / [qNd (Na + Nd)]}1/2,
откуда полная толщина p-n- перехода:
LP-n = XP + Xn = [2 εε0 (φK ± U) (Na + Nd)] /(q Na Nd)]1/2. (1.27)
Необходимо помнить, что при вычислении толщины р-n- перехода поле контактной разности потенциалов находится в противофазе с внешним полем для прямого включения и эти поля суммируются в случае обратного включения.
Дата добавления: 2015-05-13; просмотров: 1296;
