Передача информации и сообщения

Важным свойством информации является возможность ее передачи. Для этого используются сообщения- материально реализованные представления информации, нередко определенным образом закодированной. Пример сообщения - обычное письмо на бумаге.

Простейший канал передачи информации содержит три основные компоненты: передатчик информации, линию передачи информации и приемник информации.

Передатчик преобразует информацию в некоторый сигнал (электрический, оптический, электромагнитный и т. д.), который способен распространяться по линии связи. Линии связи могут быть проводными и беспроводными. Приемник принимает сигнал и преобразует его в информацию, адекватную исходной.

Существует 3 режима передачи сообщений:

Симплексный режим - передача данных только в одном направлении.

Примером симплексного режима передачи (рис.1) является система, в которой информация, собираемая с помощью датчиков, передается для обработки на ЭВМ. В вычислительных сетях симплексная передача практически не используется.

Рис. 1. Симплексный метод передачи

Полудуплексный режим - попеременная передача информации, когда источник и приемник последовательно меняются местами (рис. 2).

Яркий пример работы в полудуплексном режиме - разведчик, передающий в Центр информацию, а затем принимающий инструкции из Центра.

Рис. 2. Полудуплексный метод передачи

Дуплексный режим - одновременные передачи и прием сообщений.

Дуплексный режим (рис. 3) является наиболее скоростным режимом работы и позволяет эффективно использовать вычислительные возможности быстродействующих ЭВМ в сочетании с высокой скоростью передачи данных по каналам связи. Пример дуплексного режима - телефонный разговор.

Рис. 3. Дуплексный метод передачи

Люди научились быстро передавать информацию с помощью электрического тока в проводах (проводные линии связи), радиоволн (беспроводные линии радиосвязи) и света (оптические лазерные и световолоконные линии связи). При этом передается информация без такого привычного нам носителя, как бумага.

Наступил век безбумажнойобработки информации, хотя, в конечном счете, информационные сообщения всегда можно распечатать печатающим устройством - принтером. Любопытно, что в результате внедрения безбумажной технологии, объем выпуска бумаги, причем ее лучших сортов, для печатающих и копировальных устройств, в ведущих странах мира резко возрос.

Передача сообщений на дальние расстояния привела к возникновению телекоммуникаций. Под ними понимается и управление различными устройствами и системами на расстоянии.

А на смену обычной почте пришла электронная почта, входящая во всемирную компьютерную сеть Интернета. По электронной почте ныне можно передавать не только объемные текстовые материалы, но и звуки, изображения, рисунки и даже видеофильмы.

В теории информации (Дмитриев В.И.) изучаются количественные закономерности передачи, хранения и обработки информации.

Основное внимание в теории информации уделяется определению средней скорости передачи информации и решению задачи максимизации этой скорости путем применения соответствующего кодирования. Предельные соотношения теории информации позволяет оценить эффективность различных систем связи и установить условия согласования в информационном отношении источника с каналом и канала с потребителем.

Для исследования этих вопросов с общих позиций необходимо прежде всего установить универсальную количественную меру информации, не зависящую от конкретной физической природы передаваемых сообщений. Когда принимается сообщение о каком-либо событии, то наши знания о нем изменяются. Мы получаем при этом некоторую информацию об этом событии. Сообщение о хорошо известном нам событии, очевидно, никакой информации не несет. Напротив, сообщение о малоизвестном событии несет много информации.

Таким образом, количество информации в сообщении о некотором событии существенно зависит от вероятности этого события. Вероятностный подход и положен в основу определения меры количества информации. Для количественного определения информации, в принципе, можно использовать функцию вероятности F [P(a)], где P(a) – вероятность сообщения. Простейшей из них является функция F = 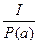, которая характеризует меру неожиданности (неопределенности) сообщения. Однако для удобства принято исчислять количество информации в логарифмических единицах, т.е. определять количество информации в отдельно взятом сообщении как:

.

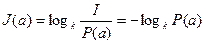При P(a)= 1 количество информации равно нулю, т.е. сообщение об известном событии никакой информации не несет. Логарифмическая мера обладает естественным в данном случае свойством аддитивности, согласно которому количество информации, содержащейся в нескольких независимых сообщениях, равно сумме количества информации в каждом из них.

Основание логарифма k может быть любым. Чаще всего принимают k=2, и тогда количество информации выражается в двоичных единицах:

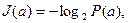дв.ед.

Двоичную единицу называют бит. В двоичных системах передачи информации используется два символа, условно обозначаемых 0 и 1. В таких системах при независимых и равновероятных символах, когда P(0)=P(1)=½, каждый из них несет одну двоичную единицу информации:

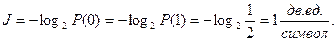
Формула позволяет вычислить количество информации в сообщениях, вероятность которых отлична от нуля. В общем случае при передачи сообщений неопределенность снимается не полностью.

В технических системах это связано с наличием помех и шумов в канале связи, которые приводят к ошибкам. В случае обучения потеря информации в канале: «источник информации – человек» объясняется неадекватностью восприятия, связанную, прежде всего, с индивидуальными способностями человека.

Таким образом, по принятому сигналу 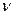только с некоторой вероятностью 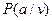< 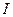можно судить о том, что было передано сообщение 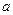, подобно тому, как преподаватель по ответам студента на экзамене или зачете может судить об объеме и качестве преподаваемого материала. Поэтому после получения сообщения остается некоторая неопределенность, характеризуемая величиной апостериорной (послеопытной) вероятности 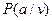, а количество информации, содержащееся в сообщении 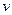, определяется степенью уменьшения неопределенности при его приеме. Если 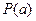- априорная вероятность, то количество информации в принятом сообщении относительно переданного сообщения 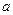, очевидно, будет равно:

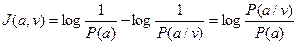
(термин априорная указывает на то, что предположение о классе объекта делается без каких либо предварительно заданных условий)

В приложении к процессу обучения это выражение предлагается рассматривать как разность между количеством информации содержащейся в источнике информации (учебнике, лекции и т.п.), и тем количеством информации, которое потеряно в процессе обучения. При этом возникает потребность оценивать количество информации не только в отдельных сообщениях, но оценивать информационные свойства источника сообщений в целом (информативность лекции, раздела книги, семинарских занятий и т.п.).

Одной из важных характеристик такого рода является среднее количество информации, приходящееся на одно сообщение.

В простейшем случае, когда все сообщения равновероятны, количество информации в каждом из них одинаково и определяется выражением:

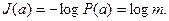
При этом среднее количество информации равно 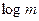. Следовательно, при равновероятных независимых сообщениях информационные свойства источника зависят только от числа сообщений в ансамбле m.

Однако в реальных условиях сообщения, как правило, имеют разную вероятность. Так, например буквы алфавита О, Е, А встречаются в тексте сравнительно часто, а буквы Щ, Ы, Ъ – редко. Поэтому знание числа сообщений m в ансамбле является недостаточным, необходимо иметь сведения о вероятности каждого сообщения: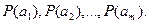

Так как вероятности сообщений неодинаковы, то они несут различное количество информации: 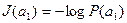. Менее вероятные сообщения несут большее количество информации и наоборот. Среднее количество информации, приходящееся на одно сообщение источника, определяется как математическое ожидание :

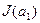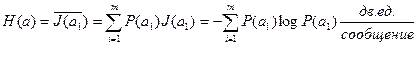(2.5)

Величина 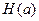называется энтропией, которая в теории информации характеризует неопределенность ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений ансамбля источника будет передано. Для нас самым существенным является то, что чем больше энтропия, тем сильнее неопределенность и тем большую информацию в среднем несет одно сообщение источника.

Статистическая связь ожидаемого сообщения с предыдущим сообщением количественно оценивается совместной вероятностью 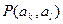или условной вероятностью 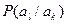, которая выражает вероятность появления сообщения 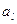при условии, что известно предыдущее сообщение 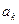. Количество информации, содержащейся в сообщении при условии, что известно предыдущее сообщение 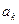будет равно:

.

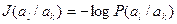Под этим нами понимается степень связи предыдущего материала в лекции с последующим.

Среднее количество информации при этом определяется условной энтропией 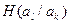, которая вычисляется как математическое ожидание информации 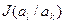по всем возможным сообщениям 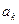и .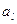

Важным свойством условной энтропии источника зависимых сообщений является то, что при неизвестном количестве сообщений в ансамбле источника его энтропия уменьшается с увеличением числа сообщений, между которыми существует статистическая взаимосвязь. В соответствии с этим свойством, а также свойством энтропии источника независимых сообщений можно записать неравенства:

.

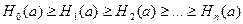Таким образом, наличие статистических связей между сообщениями всегда приводит к уменьшению количества информации, приходящейся в среднем на одно сообщение