Иллюстрация компонентов учебной деятельности

Печатается по изданию: Давыдов В.В.

Теория развивающего обучения. - М., 1996. - С. 165-168.

Теперь целесообразно на конкретном примере дать иллюстрацию таких важных компонентов учебной деятельности, как учебная задача и учебные действия, общая психологическая характеристика которых была приведена выше. Сделаем это на материале изучения детьми одного из фундаментальных понятий всего школьного курса математики – понятия числа в 1 классе.

Главная цель этого курса состоит в том, чтобы к концу средней школы сформировать у учащихся полноценную концепцию действительного числа, основой которого является понятие величины. Наш курс начинается с введения именно этого понятия, определяемого отношениями "равно", "больше", "меньше". Ориентация на эти общие отношения позволяет ребенку осуществлять разностное сравнение предметно представленных величин. Еще до усвоения понятия числа он может фиксировать результаты этого сравнения с помощью таких буквенных формул, как a = b; а > b; а < b, и производить многие из преобразований типа: а + с = b; а = b – с; а + с = b + с и т.д., опираясь на соответствующие свойства указанных отношений.

Однако в некоторых ситуациях трудно или вовсе невозможно выполнить непосредственное разностное сравнение и сразу обнаружить, например, равенство или неравенство наличных величин (отрезков, грузов и т.д.). Учитель демонстрирует первоклассникам подобные ситуации и про­сит их найти подходящий способ решения задачи. Дети выдвигают разные гипотезы и с помощью учителя приходят к выводу о том, что в данных ситуациях нужно выполнять опосредствованное сравнение. Но что это такое? С помощью каких средств его можно выполнить? Как оперировать с такими средствами и к каким результатам это приводит? Учитель сначала подводит детей к постановке перечисленных вопросов, а затем ставит перед ними учебную задачу, требующую открытия и усвоения ими общего способа опосредованного разностного сравнения величин, опирающегося на их предварительное кратное сравнение с помощью числа.

Учебные действия, позволяющие решить данную задачу, направлены на поиск, обнаружение и изучение детьми свойств, характеризуют кратное отношение величин, фиксация которого в модели как раз и обозначает число (в принципе - действительное число, хотя отдельные виды чисел предполагают наличие особых условий реализации кратного отношения и построения его модели).

Первое учебное действие состоит в принятии ребенком учебной задачи, поставленной учителем.

При выполнении второго учебного действия дети осуществляют такое предметное преобразование величин, при котором в них обнаруживается кратность отношений. При этом ребенок находит некоторую третью величину (мерку), с помощью которой можно установить кратность двух исходных величин, требующих разностного сравнения. Например, величины А и В не могут быть сравнены непосредственно (так, отрезки не могут быть непосредственно наложены друг на друга). 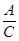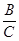Условия задачи преобразуются ребенком так, что он находит некоторую величину С, применение которой позволит ему определить, сколько раз эта величина С «укладывается» в величинах А и В, позволяет ребенку определить их кратное отношение, которое можно записать с помощью формул и (черта между буквами обозначает кратность).

Третье учебное действие связано с моделированием процесса выделения кратного отношения и его результата. В данном случае это моделирование осуществляется при единстве предметной, графической и буквенной форм. Так, первоначально кратное отношение может быть выражено с помощью предметных или графических палочек ("меток"), указывающих результат как отдельного "наложения'' мерки, так и всех подобных "наложений" (сколько раз данная мерка содержится в величине через их кратное отношение). Затем этот результат может быть представлен в словесной форме числительных («один, два, три … раза»), Тогда формулы кратного отношения и опосредованного разностного отношения приобретают следующий вид:

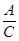= 4; 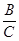=5; 4<5, А<В

В общем виде эти формулы записываются так:

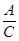= К; К < М; А < В.

Таким образом, буквенная модель процесса и результата выделения кратного отношения в общем виде выглядит так: 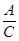= N. Благодаря этой общей формуле дети могут выделять и фиксировать любое кратное отношение величин, выражаемое в соответствующем конкретном числе (например, при данных А и С отношение изображается числом 4). По соотношению самих этих чисел (т.е. по свойствам числа как модели кратного отношения) можно опосредствованным путем решить исходную задачу разностного сравнения.

Четвертое учебное действие состоит в таком преобразовании самой модели выделенного отношения, которое позволяет изучать его общие свойства. Так, изменение мерки С при той же исходной величине А приводит к изменению конкретного числа, изображающего их отношение. Поэтому, например, есл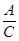и =К и

В < С, то 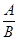> К и т.д.

Усвоение детьми содержания и следствий этого учебного действия имеет первостепенное значение при их знакомстве с миром чисел и становится характерной чертой решения именно учебной задачи, когда некоторые общие свойства чисел изучаются детьми до ознакомления с многообразием их частных проявлений.

Пятое учебное действие направлено на конкретизацию общего способа выявления кратного отношения и на решение частных задач, предполагающее поиск и фиксацию конкретных чисел, характеризующих отношения вполне определенных величин (например, нахождение числовой характеристики той или иной непрерывной или дискретной величины при данной мерке). Это действие позволяет детям связать общий принцип получения числа с частными условиями сосчитывания совокупностей или измерения непрерывных объектов. При этом подлинное понимание числа обнаруживается в том, что ребенок может свободно переходить от одной мерки к другой при определении числовой характеристики того же объекта, а тем самым соотносить с ним разные конкретные числа (одна и та же величина может быть соотнесена с самыми разными конкретными числами).

Таким образом, дети решают исходную учебную задачу путем построения общего способа получения числа и одновременно усваивают его понятие. Теперь они могут применять этот способ и соответствующее ему понятие в самых разных жизненных ситуациях, требующих определения числовых характеристик объектов.

Еще одно учебное действие - контроль позволяет детям при сохранении общей формы и смысла предыдущих четырех действий изменять их операционный состав в зависимости от частных условий их применения, от конкретных особенностей их материала (благодаря этому действия становятся умениями и навыками). Действие оценки на всех стадиях решения школьниками учебной задачи нацеливает другие их учебные действия на конечный результат - на получение и использование числа как особого средства сопоставления величин.

Мы кратко обрисовали те учебные действия, которые позволяют детям усвоить понятие числа на основе содержательного (теоретического) обобщения. В процессе реального обучения эти действия, конечно, имеют более сложное строение, описание которого предполагает и более детальную характеристику учебной деятельности на уроках математики.