Опис експериментальної установки та методу дослідження. Питомим зарядом електрона називають відношення заряду електрона до його маси

Питомим зарядом електрона називають відношення заряду електрона до його маси 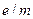. У роботі відношення 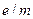для електрона визначається за допомогою методу, що одержав назву «методу магнетрона». Ця назва пов'язана з тим, що конфігурація електричних і магнітних полів (ці поля взаємно перпендикулярні), які використовуються в цій роботі, подібна до конфігурації полів у магнетронах – генераторах електромагнітних коливань в області надвисоких частот. Перпендикулярність електричних і магнітних полів є основною ознакою магнетрона.

У цій лабораторній роботі як магнетрон використовується двохелектродна лампа, яка міститься в магнітному полі соленоїда (рис. 4.3.1). Нитка розжарення лампи (катод) (рис. 4.3.1, позиція 2) розміщується вздовж осі циліндричного анода (рис. 4.3.1, позиція 1); таким чином електричне поле спрямоване вздовж радіуса. Лампа міститься всередині соленоїда, що створює магнітне поле паралельне катоду та перпендикулярне до ліній напруженості електричного поля.

Розглянемо траєкторію електронів, що рухаються під дією електричного й магнітного полів у магнетроні. Для обчислень використаємо циліндричну систему координат, тобто будемо характеризувати положення точки відстанню від осі циліндра 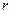, полярним кутом 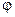і координатою 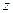уздовж осі (рис. 4.3.2).

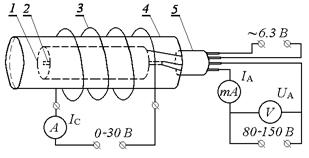
Рисунок 4.3.1 – Принципова схема експериментальної установки: 1 – анод; 2 – катод; 3 – обмотка соленоїда; 4 – скляний балон; 5 – цоколь лампи; 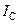– сила струму соленоїда; 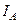– сила анодного струму; 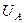– анодна напруга (анод – катод); змінна напруга 6,3 В використовується для розжарення катода

Розглянемо спочатку сили, що діють на електрон з боку електричного поля. Напруженість електричного поля, утвореного катодом і анодом, має лише радіальну компоненту 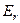. Сила, що діє на електрон у такому полі, спрямована вздовж радіуса й визначається формулою

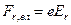. (4.3.1)

Усі інші компоненти електричних сил відсутні:

.

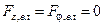Розглянемо тепер сили, що діють на електрон з боку магнітного поля. Оскільки магнітне поле в магнетроні спрямовано вздовж осі 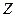, для проекції сили на вісь 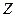маємо

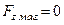. (4.3.2)

Інші дві компоненти сили знайдемо за допомогою формули для сили Лоренца. Як неважко переконатися, вони дорівнюють

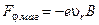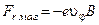, , (4.3.3)

де

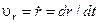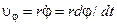, (4.3.4)

є відповідними компонентами швидкості електрона.

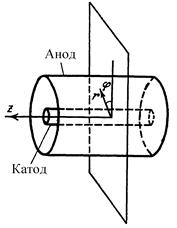
Рисунок 4.3.2 – До розрахунку рівняння руху електронів

Як було з'ясовано вище, ні магнітні, ні електричні сили, що діють на електрон, не мають складових вздовж осі 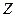. Рух уздовж осі 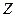є, таким чином, рівномірним. Рух у площині 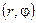зручно описувати за допомогою рівняння моментів

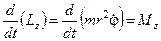, (4.3.5)

де 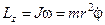– момент імпульсу електрона відносно осі 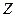. Результуючий момент сил 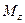відносно осі 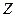дорівнює 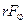. За допомогою (4.3.3) знайдемо

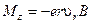. (4.3.6)

Підставляючи (4.3.4) і (4.3.6) в (4.3.5), отримуємо

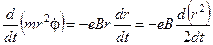. (4.3.7)

Інтегруючи рівняння (4.3.7) і беручи до уваги, що заряд електрона є від’ємним, отримуємо

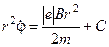, (4.3.8)

де 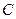– стала інтегрування, яку визначимо з початкових умов. На початку руху радіус 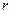дорівнює радіусу катода 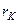. Електрони вилітають із катода з невеликою швидкістю, так що 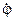в початковий момент можна взяти таким, що дорівнює нулю. Тому

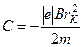. (4.3.9)

Рівняння (4.3.8) при цьому набере такого вигляду:

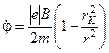. (4.3.10)

Розглянемо рух електрона вздовж радіуса. Робота електричного поля, що виконується при переміщенні електрона від катода до точки з потенціалом 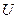, дорівнює

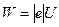. (4.3.11)

Як відомо, магнітне поле ніякої роботи не виконує. Тому робота (4.3.11) дорівнює кінетичній енергії електрона (початковою кінетичною енергією нехтуємо):

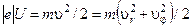. (4.3.12)

За допомогою (4.3.4) і (4.3.10) знайдемо

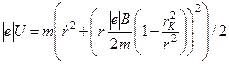. (4.3.13)

Рівняння (4.3.13) повністю визначає радіальний рух електрона.

Розглянемо тепер траєкторію електронів, що вилетіли з катода при потенціалі анода 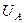. За умови відсутності магнітного поля (рис. 4.3.3) електрон рухається прямолінійно уздовж радіуса від катода до анода. Поява магнітного поля призводить до викривлення траєкторії. При деякому значенні індукції магнітного поля 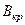, яке називають критичним, траєкторія викривлюється настільки, що торкається анода. Нарешті, при 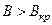електрон зовсім не потрапляє на анод і вертається до катода.

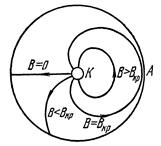
Рисунок 4.3.3 – Траєкторії електронів, що вилітають із катода при різних значеннях індукції магнітного поля

Величину 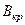неважко знайти за допомогою (4.3.13), помітивши, що у цьому разі радіальна швидкість електрона 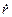біля анода ( 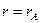, 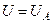) дорівнює нулю:

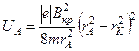. (4.3.14)

Перетворюючи (4.3.14), знайдемо

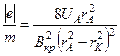. (4.3.15)

Індукція магнітного поля всередині довгого соленоїда визначається його струмом :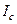

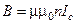, (4.3.16)

де m – магнітна проникність середовища; m₀ – магнітна стала, 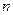– число витків на одиницю довжини соленоїда. Об’єднуючи вирази (4.3.16) і (4.3.15), остаточно отримаємо

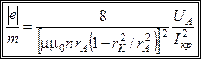, (4.3.17)

де 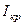– критичний струм соленоїда, при якому індукція магнітного поля є критичною .

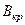Формула (4.3.17) дозволяє обчислювати 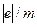, якщо при заданому 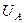знайдений критичний струм соленоїда 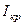, при якому електрони перестають потрапляти на анод.

Вище ми припускали, що всі електрони залишають катод зі швидкістю, яка дорівнює нулю. У цьому разі при 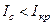або 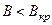усі електрони без винятку потрапляли б на анод, а при 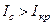або 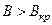усі вони поверталися б на катод, не досягнувши анода. Анодний струм 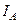зі збільшенням магнітного поля змінювався б при цьому так, як це зображено на рис. 4.3.4 пунктирною лінією. Насправді електрони, що випускаються нагрітим катодом, мають різні початкові швидкості. Критичні умови досягаються для різних електронів при різних значеннях 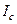. Крива 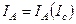набирає внаслідок цього вигляду суцільної лінії на рис. 4.3.4.

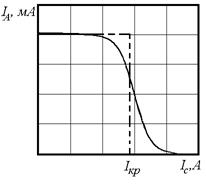
Рисунок 4.3.4 – Графік залежності анодного струму від струму соленоїда. Суцільна крива відповідає реальному випадку; пунктирна крива відповідає випадку, коли початкові швидкості електронів дорівнюють нулю

Зазначимо, крім того, що неможливо забезпечити повну коаксіальність анода й катода, тобто в реальних умовах вектор індукції магнітного поля завжди дещо нахилений відносно катода й т. д. Усі ці причини приводять до додаткового згладжування кривої рис. 4.3.4. У добре зібраній установці злам функції 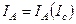залишається, однак, досить різким і може бути використаний для виміру .

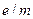У реальному експерименті можна приблизно вважати, що випадку критичного струму буде відповідати струм соленоїда, при якому спостерігається найбільш швидке зменшення анодного струму. Виходячи з цього, шукаємо критичний струм соленоїда як такий, що відповідає найбільшому куту між дотичною[17]⁾ до експериментальної кривої та горизонтальною віссю (рис. 4.3.5). На рис. 4.3.5 штриховими лініями виділено інтервал струмів, у якому знаходиться значення критичного струму. Середнє значення цього інтервалу відповідає 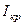, півширина його – похибці .

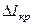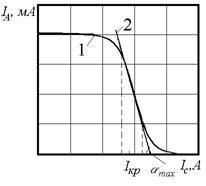
Рисунок 4.3.5 – Графік залежності анодного струму від струму соленоїда (крива 1). Крива 2 – дотична до експериментальної кривої у точці, що має максимальний кут нахилу з горизонтальною кривою 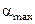. Штриховими лініями виділено інтервал струмів, у якому знаходиться значення критичного струму. Середнє значення цього інтервалу визначає 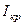, його півширина – похибку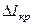

Таким чином, отримавши експериментальну залежність анодного струму 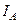від струму соленоїда 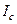, можемо визначити критичний струм 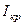. Далі, використовуючи співвідношення (4.3.17), обчислимо питомий заряд електрона .

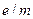Схема експериментальної установки наведена на рис. 4.3.1. Ключовим блоком цієї установки є магнетрон – сукупність двохелектродної лампи та соленоїда. За допомогою відповідної ручки регулювання можна змінювати струм соленоїда 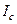. Залежно від цього буде змінюватися анодний струм 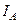. При цьому анодна напруга 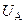є сталою величиною. Виконавши відповідні вимірювання, можна отримати необхідну залежність 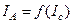. Далі з отриманої кривої знайдемо критичний струм і за допомогою (4.3.17) обчислимо питомий заряд електрона.