ЗАДАЧИ АППРОКСИМАЦИИ

Конкретное содержание обработки одномерных ЭД зависит от поставленных целей исследования. В простейшем случае достаточно определить первый момент распределения, например, среднее время обработки запросов к распределенной базе данных. В других случаях требуется установить вероятностно-временные характеристики распределения, например, оценить вероятность своевременной обработки запросов или вероятность безотказной работы системы в течение заданного периода времени. Для нахождения таких значений требуется знание закона распределения как наиболее полной характеристики соответствующей случайной величины.

В классической математической статистике предполагается известным вид закона распределения и производится оценка значений его параметров по результатам наблюдений. Но обычно заранее вид закона распределения неизвестен, а теоретические предположения не позволяют его однозначно установить. Обработка ЭД также не позволит точно вычислить истинный закон распределения показателя. В таком случае следует говорить только об аппроксимации (приближенном описании) реального закона некоторым другим, который не противоречит ЭД и в каком-то смысле похож на этот неизвестный истинный закон.

В соответствии с этими положениями постановка задачи аппроксимации закона распределения ЭД формулируется следующим образом.

Имеется выборка наблюдений (x₁, x₂, …, x_n) за случайной величиной Х. Объем выборки п фиксирован.

Необходимо подобрать закон распределения (вид и параметры), который бы в статистическом смысле соответствовал имеющимся наблюдениям.

Ограничения: выборка представительная, ее объем достаточен для оценки параметров и проверки согласованности выбранного закона распределения и ЭД; плотность распределения унимодальная.

Наличие в функции плотности распределения нескольких мод может быть следствием различных причин, например существованием различных по длине маршрутов прохождения запросов в системе обработки. Выборку с несколькими модами разделяют на составные части так, чтобы каждая из них имела одну моду. В последнем случае функция распределения исходной выборки представляет собой взвешенную сумму соответствующих функций отдельных выборок:

,

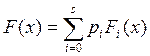где s – количество выборок, выбранное исходя из требований унимодальности распределения; p_i – вероятность принадлежности элемента выборки к выборке i; F_i(x) – функция распределения выборки i.

Решение поставленной задачи аппроксимации осуществляется на основе применения "типовых" распределений, специальных рядов или семейств универсальных распределений.