ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ВЕРОЯТНОСТИ

Пусть случайная величина Х имеет только два возможных значения: 0 и 1. В результате проведения достаточно большого количества наблюдений эта случайная величина приняла единичное значение n раз. Необходимо при заданной надежности 1–a определить доверительный интервал для вероятности р, оценка которой соответствует частоте w* = m*/n.

Оценка w* вероятности р является состоятельной, эффективной и несмещенной. Если оцениваемая вероятность не слишком мала и не слишком велика (0,05< p <0,95), то можно считать, что распределение случайной величины w* близко к нормальному. Этим допущением можно пользоваться, если пр и п(1–р) больше четырех. Параметры нормального распределения частоты m^*_x = р, S² = р(1–р)/п (дисперсия S²(m) количества успехов m составляет величину пр(1–р), а дисперсия частоты S²(m)/п². Тогда по аналогии с определением доверительного интервала для математического ожидания нормально распределенной величины w* можно записать

ε = |w*– p| = u_{1– a/2}(S² (т) )^0,5 =u_{1– a/2}(р(1–р)/п)^0,5,

где u_{1– a/2} – квантиль стандартизованного нормального распределения.

Чтобы связать доверительный интервал с исходными параметрами n, w* и u_{1– a/2}, возведем выражение для ε в квадрат, т. е. преобразуем равенство к виду

(w*–p)²=u²_{1– a/2}(1–p)p/п.

Доверительные границы можно получить, решив это уравнение второй степени

p_2,1 ={nw* + 0,5u²_{1– a/2} ± u_{1– a/2} [nw*(1–w*) + 0,25u²_{1– a/2}]^0,5}/(п + u²_{1– a/2}). (4.5)

С увеличением объема выборки (пw* >200, nw*(1–w*)>200) такими слагаемыми как u²_{1– a/2}, 0,5u²_{1– a/2} и 0,25u²_{1– a/2} можно пренебречь, тогда приближенно

p₁ =w*– u_{1– a/2} [w*(1–w*)/n]^0,5,

p² =w* + u_{1– a/2} [w*(1–w*)/n]^0,5. (4.6)

Более общие результаты получены с учетом того, что случайная величина w* распределена по биномиальному закону

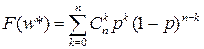(4.7)

где Cⁿ_k – число сочетаний из n по k.

Исходя из этого положения, для практического применения получены значения нижней р₁ и верхней р₂ доверительных границ

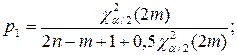(4.8)

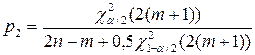. (4.9)

где 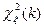– квантиль распределения хи-квадрат уровня X с числом степеней свободы k.

Формулы (4.8) и (4.9) можно применять и в тех случаях, когда частость w* события близка (равна) нулю или близка (равна) количеству экспериментов п соответственно. В первом случае НДГ р₁ принимается равной нулю и рассчитывается только ВДГ р₂. Во втором случае рассчитывается НДГ р₁, а верхняя граница р₂ =1.

Пример 4.5. В результате наблюдения за 58 изделиями не было зафиксировано ни одного отказа. Определить доверительный интервал для вероятности отказа с надежностью 0,9.

Решение. Нижнюю доверительную границу р₁ следует принять равной нулю, ВДГ

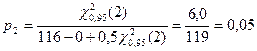
Таким образом, доверительный интервал с нижней границей 0 и верхней границей 0,05 с вероятностью 0,9 накрывает истинное значение вероятности отказа изделий.