Движение жидкости в каналах рабочего колеса центробежного насоса

Движение реальной жидкости в межлопаточных каналах рабочего колеса представляет собой весьма сложный гидромеханический процесс. Поэтому до настоящего времени уравнения движения получить чисто теоретическим путем не удается. Теоретические уравнения движения жидкости в межлопаточных каналах динамических гидромашин (лопаточных насосов и гидротурбин) получены Л.Эйлером при следующих двух допущениях:

1. Жидкость идеальная, т.е. гидравлические сопротивления не учитываются;

2. Жидкость движется в виде бесконечного числа элементарных струек, строго повторяющих форму лопаток.

Эти допущения облегчают теоретическое исследование движения жидкости в лопаточных системах, но в дальнейшем требуют внесения существенных поправок на основании экспериментальных исследований.

Движение каждой частицы жидкости потока в рабочем колесе является сложным, абсолютная скорость которой складывается из переносной и относительной скоростей. Скорость переносного движения, это линейная скорость вращательного движения точки рабочего колеса, где в данный момент находится частиц жидкости. Эта скорость направлена по касательной к окружности, на которой находится частица. Относительная скорость – это скорость перемещения частицы относительно лопатки колеса: вектор относительной скорости 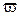направлен по касательной к лопатке.

Абсолютная скорость определяется как векторная разность:

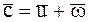
Параллелограммы скоростей на входе в межлопаточные каналы и выходе из них показаны на рисунке 3.10.

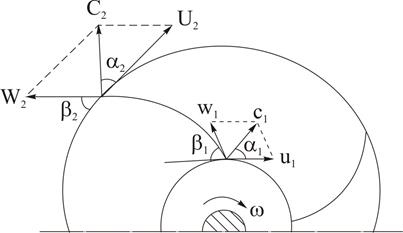
Рисунок 3.10

Все величины на входе обозначаются с индексом 1, а на выходе – 2.

Если угловая скорость вращения рабочего колеса ω, т.е. окружные линейные скорости будут равны

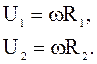
Векторы относительных скоростей W₁ и W₂ направлены по касательной к стенкам лопаток рабочего колеса.

Углы, определяющие форму лопатки рабочего колеса, обозначаются β₁ и β₂ - это углы между направлением относительной скорости W и в обратном направлении окружной скорости (-U).

Углы между направлением абсолютной скорости С и окружной скорости U обозначаются α₁ и α ₂ (рисунок 3.10).

Из уравнения неразрывности потока жидкости, протекающего через рабочее колесо, следует:

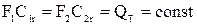
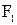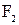где C_1r и C_2r - радиальные составляющие абсолютных скоростей на входе и выходе, а площади сечения и представляют собой поверхности вращения с образующей, нормальной к радикальной скорости. Обычно вместо параллелограммов скоростей строят треугольники скоростей (рисунок 3.11).

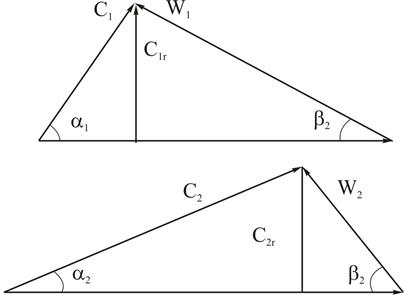
Рисунок 3.11

Площади сечений 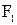и F₂ равны:

на входе: ,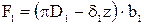

на выходе: ,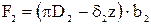

где 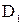и 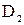– соответственно диаметры на входе в межлопаточные каналы и выходе из них; 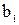и 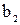– ширина лопатки (канала); 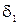и 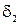– толщина лопаток, z - число лопаток.

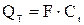– представляет собой идеальную подачу рабочего колеса центробежного насоса.