Выполнение арифметических операций

Основной операцией, которая используется в цифровых устройствах при различных вычислениях, является операция алгебраического сложения чисел (сложения в котором могут участвовать как положительные, так и отрицательные числа). Такие операции как умножение и деление также выполняются с помощью операции сложения и некоторых логических операций (например, сдвига результата сложения). Поэтому с операции сложения начнем рассмотрение выполнения арифметических операций микропроцессором.

Сложение положительных двоичных чисел. Выполнение этой операции покажем на примере:

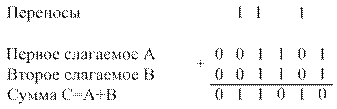
Цифры разрядов суммы формируются последовательно, начиная с младшего разряда. Цифра младшего разряда суммы получается суммированием цифр младших разрядов слагаемых. При этом, кроме цифры разряда суммы формируется цифра переноса в следующий более старший разряд. Таким образом, в разрядах, начиная со второго, суммируются три цифры: цифры соответствующего разряда слагаемых и перенос, поступающий в данный разряд из предыдущего.

Перенос равен 1 во всех случаях, когда результат суммирования цифр в разряде равен или больше 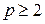(основание системы счисления). При этом в разряд суммы записывается цифра на 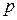единиц (т.е. на 2 единицы) меньшая результата сложения.

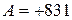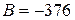Алгебраическое сложение с использованием дополнительного кода. Для пояснения сущности излагаемого метода рассмотрим следующий пример. Пусть необходимо сложить два десятичных числа и . Так как второе слагаемое отрицательное число, то согласно приему, известному из школьной программы, для получения цифр суммы потребуется заем из старших разрядов. В цифровом устройстве эту операцию выполнять не обязательно. Искомый результат может быть получен, если отрицательное число преобразовать в дополнительный код и выполнить операцию поразрядного сложения (как при сложении положительных чисел).

При сложении складываются и двоичные цифры знаковых разрядов с отбрасыванием возникающего из этого разряда переноса.

Дополнительный код отрицательного числа формируется по следующему правилу: инвертируются (производится замена 0 на 1 и 1 на 0) цифры всех разрядов отрицательного числа, кроме знакового разряда, и в младший разряд прибавляется 1. Например, если 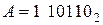, то 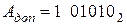. Обратное преобразование из дополнительного кода в прямой код производится по тому же правилу.

Рассмотрим примеры выполнения операции сложения.

Пример 1. Пусть 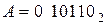и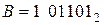

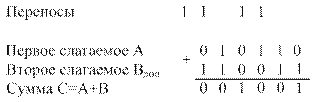
Как указывалось выше, перенос из знакового разряда отбрасывается.

Пример 2. Изменим знаки слагаемых (по отношению к предыдущему примеру) 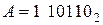и .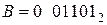

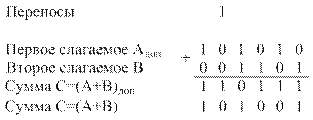
Таким образом, если результат сложения есть отрицательное число, то оно оказывается представленным в дополнительном коде.

Сложение десятичных чисел. Двоично-десятичные числа суммируются по правилам сложения двоичных чисел. Если при суммировании цифр тетрады полученная сумма больше девяти или формируется перенос из старшего разряда тетрады, то выполняется коррекция результата. При этом к полученной сумме прибавляется число шесть.

Пример 1. Сложить десятичные числа А=18 и В=19.

При суммировании отрицательных десятичных чисел отрицательные числа должны быть представлены в дополнительном коде. Дополнительный код отрицательного десятичного числа получается путем замены цифр разрядов (кроме знакового разряда) их дополнением до 9 и прибавлением затем в младший разряд 1. Например, если 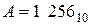, то 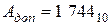. При представлении десятичных чисел двоично-десятичным кодом 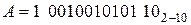дополнительный код получается следующим образом: сначала во все тетрады добавляется 0110₂ (6),

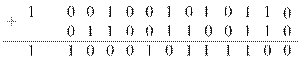
затем все цифры разрядов (кроме знакового разряда) инвертируются, и к младшему разряду прибавляется 1

Пример 2. Сложить десятичные числа А=836 и В=-256.

Умножение двоичных чисел. Операция умножения включает определение знака и абсолютного значения произведения.

Знаковый разряд произведения может быть получен суммированием по модулю 2 знаковых разрядов сомножителей.

Абсолютное значение произведения получается путем перемножения чисел без учета их знаков.

Пусть производится умножение чисел 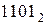и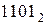

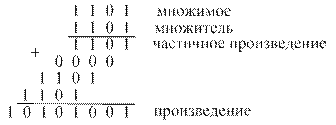
Как видно из примера, операция умножения состоит из ряда последовательных операций сложения частичных произведений. Операциями сложения управляют разряды множителя: если в каком-то разряде множителя находится единица, то к сумме частичных произведений добавляется множимое с соответствующим сдвигом; если в разряде множителя – нуль, то множимое не прибавляется. Процесс суммирования можно начинать с младшего либо старшего частичного произведения.

Ниже показаны процессы при умножении с суммированием частичных произведений, начиная со старшего (используется приведенный выше пример умножения чисел 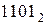и ).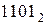

При умножении целых чисел для фиксации произведения в разрядной сетке должно предусматриваться число разрядов, равное сумме чисел разрядов множимого и множителя.