Методические указания к решению задачи
Как отмечалось в методических указаниях к задаче 1. ное напряжение внутренней изоляции зависит от времени приложения напряжения. Вид этой зависимости имеет сложный характер, так как при разных временах процессы визоляции, приводяцие кпробою, имеют различную физическую природу. Следует отметить, что при любом значении времени пробивное напряжение - величина случайная имеющая определенное поле разброса, что объясняется природой процессов при пробое и наличием неконтролируемых случайных различий между однотипными изоляционными конструкциями.
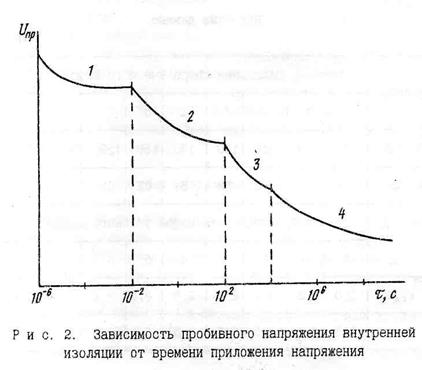
Характерная форма зависимости пробивного напряжения внутренней изоляции Uпр от времени приложения напряжения х показана на рис. 2. Зависимость 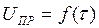 может быть разделена на несколько участков, характерных физической природой процессов пробоя, На рис. 2 границы этих участков указаны ориентировочно и зависят от размеров, свойств и условий работы изоляции.
может быть разделена на несколько участков, характерных физической природой процессов пробоя, На рис. 2 границы этих участков указаны ориентировочно и зависят от размеров, свойств и условий работы изоляции.
|
Рис. 2. Зависимость пробивного напряжения внутренней изоляции от времени приложения напряжения
Участок 1 зависимости 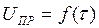 - зона чисто электрического пробоя. Он охватывает диапазон порядка 10 -6...10 -2 с (от нескольких микросекунд до нескольких миллисекунд). Электрический пробой связан с процессом образования и увеличения числа свободных электронов, вследствие чего возникает концентрированный поток электронов и в изоляции образуется проводящий канал. В начальной области этого участка пробивное напряжение увеличивается с уменьшением х, что связано с необходимостью обеспечения определенной скорости движения электронов для возникновения пробоя. При временах более 10м пробивное напряжение остается практически неизменным, так как время много больше времени формирования проводящего канала, а другие механизмы пробоя еще не проявляются.
- зона чисто электрического пробоя. Он охватывает диапазон порядка 10 -6...10 -2 с (от нескольких микросекунд до нескольких миллисекунд). Электрический пробой связан с процессом образования и увеличения числа свободных электронов, вследствие чего возникает концентрированный поток электронов и в изоляции образуется проводящий канал. В начальной области этого участка пробивное напряжение увеличивается с уменьшением х, что связано с необходимостью обеспечения определенной скорости движения электронов для возникновения пробоя. При временах более 10м пробивное напряжение остается практически неизменным, так как время много больше времени формирования проводящего канала, а другие механизмы пробоя еще не проявляются.
Участок 2 {диапазон времени 10 -2...10 2- от сотых долей секунды до десятков секунд) характерен для изоляции с наличием жидкого диэлектрика. Здесь наблюдается снижение электрической прочности при увеличении т, что связано с образованием проводящих мостиков из примесей.
Следующий участок 3 - область теплового пробоя, который связан с нарушением тепловой устойчивости изоляции. Этот участок охватывает диапазон времени 102..10 4 {от десятков секунд до нескольких часов).
Наконец, последний участок 4 зависимости 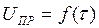 - электрическое старение изоляции, то есть необратимое ухудшение диэлектрических свойств под действием электрических полей. Процессы электрического старения могут протекать от нескольких часов до 10-15 лет и более.
- электрическое старение изоляции, то есть необратимое ухудшение диэлектрических свойств под действием электрических полей. Процессы электрического старения могут протекать от нескольких часов до 10-15 лет и более.
Задача обеспечения длительной электрической прочности внутренней изоляции в процессе старения, то есть требуемого срока ее службы, является одной из наиболее сложных. Это связано с тем, что прямым экспериментом нельзя определить ход зависимости ипр = Их) в области больших времен, так как для этого потребовались бы десятилетия. Поэтому при решении данной задачи используются косвенные методы, основанные на измерении истенсивности процессов, вызывающих старение.
Причиной старения внутренней изоляции могут быть воздействия различной физической природы. В основном это электрические, тепловые и механические нагрузки. Соответственно различают электрическое, тепловое и механическое старение внутренней изоляции. Кроме того, старение может быть обусловлено проникновением загрязнений, увлажнением изоляции.
В данной задаче контрольной работы производится расчет срока службы внутренней изоляции с учетом электрического и теплового старения.
Основной причиной электрического старения внутренней изоляции являются частичные разряды. Частичными разрядами называют разрядные процессы в изоляции, которые развиваются под действием приложенного напряжения и распространяются лишь на часть изоляционного промежутка.
Частичные разряды возникают в ослабленных местах изоляции, например в газовых включениях или в местах резкого усиления электрического поля. Наибольшую опасность представляют частичные разряды в газовых включениях, так как в этом случае они возникают при меньших напряжениях, чем в жидких и твердых компонентах изоляции.
Темпы электрического старения возрастают с увеличением приложенного к изоляции напряжения, а сроки службы соответственно уменьшаются. При этом зависимость срока службы т от величины напряжения может иметь сложный характер.
Экспериментальные исследования показали, что для относительно небольшого времени (до 10 3...104 час) график зависимости среднего срока службы внутренней изоляции от приложенного напряжения 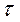 = f(U), построенный б двойном логарифмическом масштабе, то есть
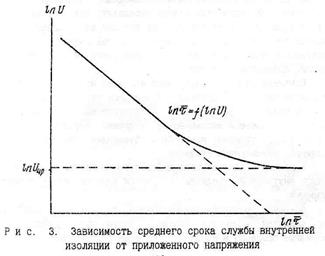
= f(U), построенный б двойном логарифмическом масштабе, то есть 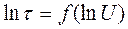 , имеет вид прямой линии (рис.3). Установлено также, что в области больших времен по мере снижения напряжения сроки службы увеличиваются быстрее, чем по указанной зависимости, а ниже некоторого уровня напряжения становятся неограниченно длительными, что также иллюстрируется графиком на рис.3. Этот уровень является напряжением появления в изоляции частичных разрядов.
, имеет вид прямой линии (рис.3). Установлено также, что в области больших времен по мере снижения напряжения сроки службы увеличиваются быстрее, чем по указанной зависимости, а ниже некоторого уровня напряжения становятся неограниченно длительными, что также иллюстрируется графиком на рис.3. Этот уровень является напряжением появления в изоляции частичных разрядов.
|
Рис. 3. Зависимость среднего срока службы внутренней
изоляции от приложенного напряжения
Такому ходу зависимости 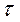 = f(U) качественно соответствует выражение
= f(U) качественно соответствует выражение
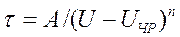
где Uчр - напряжение появления в изоляции частичных разрядов, кВ;
А - постоянная, зависящая от свойств изоляции, в расчетах при решении задачи 2 контрольной работы следует принять типичное для твердой изоляции при нормальных условиях значение А = 6-109 год/(кВ)п;
п - показатель степени, зависящий от конструктивных особенностей изоляции и рода воздействующего напряжения; в большинстве видов изоляции при напряжении промышленной частоты п = 4...8, в контрольной работе принять п = 6.
Как уже отмечалось, между любыми однотипными изоляционными конструкциями существуют неконтролируемые случайные различия, поэтому при заданных условиях эксплуатации срок службы изоляционной конструкции есть величина случайная и приведенное выражение дается среднее значение. Следует отметить, что разбросы величины срока службы изоляции относительно среднего значения могут быть значительными.
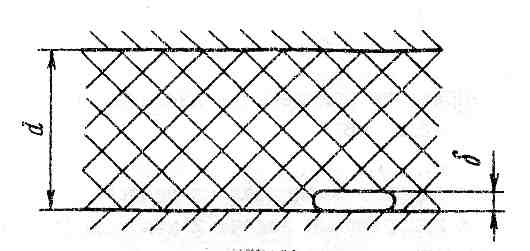
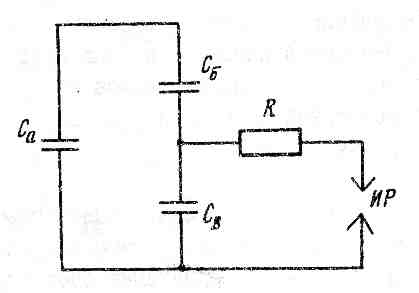
Для расчета среднего срока служба изоляции по приведенной выше формуле необходимо знать напряжение возникновения частичных разрядов Uчр. Для его определения изоляцию с газовым включением условно изобразим в виде рис. 4. На этом рисунке d - толщина слоя внутренней изоляции, 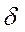 - толщина газового включения, в котором могут возникать частичные разряды. Схема замещения для случая переменного напряжения может быть представлена, как показано на рис. 5. где СВ - емкость газового включения, С\Б - емкость участка изоляции, расположенного последовательно с газовым включением, Св - емкость остальной части изоляции, ИР - искровой разрядник, имитирующий пробой газового включения, R -- сопротивление канала частичных разрядов в газовом включении.
- толщина газового включения, в котором могут возникать частичные разряды. Схема замещения для случая переменного напряжения может быть представлена, как показано на рис. 5. где СВ - емкость газового включения, С\Б - емкость участка изоляции, расположенного последовательно с газовым включением, Св - емкость остальной части изоляции, ИР - искровой разрядник, имитирующий пробой газового включения, R -- сопротивление канала частичных разрядов в газовом включении.
|
Рис. 4. Изоляция с газовым включением
|
Рис. 5. Схема замещения изоляции с газовым включением
Для расчета величин С6 и Св можно воспользоваться формулой для емкости плоского конденсатора. Тогда получим:
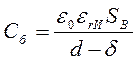
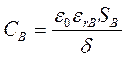 ;
;
где SВ - площадь сечения газового включения, перпендикулярного силовым линиям электрического поля;
и 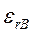 ,
, 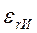 - относительные диэлектрические проницаемости соответственно заполняющей включение среды и изоляции;
- относительные диэлектрические проницаемости соответственно заполняющей включение среды и изоляции; 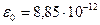 Ф/м - электрическая постоянная. . .
Ф/м - электрическая постоянная. . .
При приложении к изоляции переменного напряжения частичные разряды будут возникать, если амплитуда напряжения на емкости Св будет больше пробивного напряжения газового включения (разрядника ИР по схеме рис. 5) UB!ip. Это условие соблюдается, если величина напряжения на изоляции (действующее значение) будет равна:
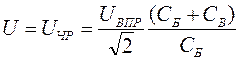
После подстановки выражений для емкостей Сй и Св и упрощенийс учетом того, что 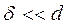 , получим:
, получим:
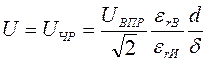
Данная формула имеет место для изоляции с однородным электрическим полем. Более характерным является случай с неоднородным полем во внутренней изоляции. Очевидно, что тогда наименьшая величина напряжения Uчр будет, если газовое включение находится в области наибольшей напряженности электрического поля. Эта величина будет равна:
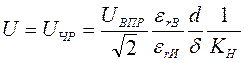
где Кн - коэффициент неоднородности электрического поля в изоляции, равный отношению максимальной напряженности средней напряженности поля.
При._ малых размерах газовых включений, что имеет место на практике, пробивное напряжение Uвнр слабо зависит от размеров включения и равно для воздуха примерно ЗО0 В.
Так как размеры газового включения и место его расположения в изоляции случайны, то для однотипных изоляционных конструкций будут иметь место значительные разбросы напряжения Uчр.
Тепловое старение изоляции есть следствие возникновения или ускорения химических реакций в диэлектрических материалах при повышении температуры. Химические реакции приводят к постепенному изменению структуры и свойств материалов и как следствие к ухудшению свойств изоляций в целом.
Влияние нагревания на различные изоляционные материалы различно. Однако для твердых диэлектриков характерным является снижение механической прочности в процессе теплового старения. Со временем это приводит к повреждению изоляции под действием механических нагрузок и затем уже к пробою.
Темпы теплового старения внутренней изоляции определяются скоростями химических реакций. Для практики можно принять, что срок службы изоляции обратно пропорционален скорости химических реакций. Тогда отношение сроков службы изоляции при различных температурах будет равно:
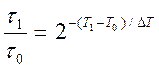
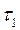 и
и 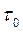 to - сроки службы соответственно при температурах Т1 и То;
to - сроки службы соответственно при температурах Т1 и То; 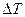 -- повышение температуры, вызывающее сокращение срока службы изоляции при тепловом сохранении в 2 раза.
-- повышение температуры, вызывающее сокращение срока службы изоляции при тепловом сохранении в 2 раза.
Данное выражение является следствием известного из химии уравнения Аррениуоа при указанном допущении. Значение 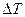 для разных используемых в технике видов внутренней изоляций лежит в пределах от 8 до 12°С и в среднем составляет 10°С. Это среднее значение следует принять для расчетов в контрольной работе. Используя приведенное выражение можно, зная срок службы изоляции при нормальной температуре , определить срок службы при любой температуре.
для разных используемых в технике видов внутренней изоляций лежит в пределах от 8 до 12°С и в среднем составляет 10°С. Это среднее значение следует принять для расчетов в контрольной работе. Используя приведенное выражение можно, зная срок службы изоляции при нормальной температуре , определить срок службы при любой температуре.
Приведенное выражение для сроков служба изоляции при тепловом старении дает достаточную для практики точность. В то же время вследствие сложности химических процессов и влияния на них большого числа факторов строгий расчет сроков службы внутренней изоляции при тепловом старении затруднителен.
Порядок оформления задачи
1. Расчет появления в изоляции частичных разрядов Uпр.
2. Расчет среднего срока службы изоляции при нормальной температуре т0-
3. Расчет зависимости среднего срока службы изоляции от температуры т - f(t). Расчет произвести в диапазоне температур от 20 до 50°С с шагом 10°С.
4. Построение графика зависимости 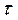 - f{t).
- f{t).
Дата добавления: 2015-04-01; просмотров: 1691;