Удельные объемы жидкости и пара.
Удельный объем жидкости зависит от температуры и давления. Однако последняя зависимость настолько незначительна, что практически ею пренебрегают.
Зависимость же удельного объема воды от температуры более заметна. Так, например, если при 0 оС и любом давлении удельный объем жидкой кипящей воды v’0 = 0,001 м3/кг, то при температуре 100 оС (и давлении ~ 1 ата) v’ = 0,001043 м3/кг, а при температуре 200 оС (и давлении ~ 16 ата) v’ = 0,001156 м3/кг.
Из этих данных следует, что при невысоких давлениях (точнее температурах) и этой зависимостью также можно пренебрегать, полагая, следовательно, что v’ = v’0 = 0,001 м3/кг.
Удельный объем сухого пара 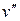 может быть найден для давлений до 10 ата по следующей формуле, полученной на основании опытов:
может быть найден для давлений до 10 ата по следующей формуле, полученной на основании опытов:
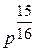 v” = 1,7235, (5.1)
v” = 1,7235, (5.1)
откуда
v” 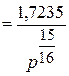 . (5.2)
. (5.2)
Здесь р берется в ата.
Из этой формулы видно, что чем больше давление сухого пара, тем удельный объем его меньше, вследствие чего и отрезки 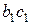 ,
, 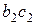 и т.д. (рис. 5.1) с повышением давления уменьшаются. Так как v”
и т.д. (рис. 5.1) с повышением давления уменьшаются. Так как v” 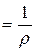 , где
, где 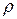 – плотность сухого пара, то, подставляя это значение v”в уравнение (5.1), получим, что
– плотность сухого пара, то, подставляя это значение v”в уравнение (5.1), получим, что
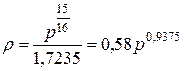 . (5.3)
. (5.3)
Приближенно можно полагать, что при р около 10–15 ата  0,5 р,
0,5 р,
т.е., что плотность сухого пара численно равен половине давления.
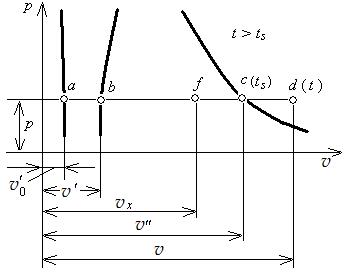
Рис. 5.6. Изображение удельных объемов воды в осях vр
при различных ее состояниях
Удельный объем влажного пара  находится в пределах между v’ и v” (рис. 5.6). Величина его зависит от степени сухости пара х. Если в 1 кг влажного пара содержится х кг сухого пара и (1 – х) кг воды, то эти х кг сухого пара будут занимать объем х v” м3/кг, а (1 – х) кг воды (1 – х) v’ v’м3/кг.
находится в пределах между v’ и v” (рис. 5.6). Величина его зависит от степени сухости пара х. Если в 1 кг влажного пара содержится х кг сухого пара и (1 – х) кг воды, то эти х кг сухого пара будут занимать объем х v” м3/кг, а (1 – х) кг воды (1 – х) v’ v’м3/кг.
Следовательно,
vх = х v”+ (1–х) v’ м3/кг. (5.4)
Так как влажный пар, применяемый в теплотехнике, имеет обычно большую степень сухости (порядка 0,9 и больше), то объемом воды, содержащейся в нем, можно пренебрегать, считая, что
vх ≈ х v” м3/кг. (5.5)
Неточность, допускаемая при этом, получается незначительной.
При небольшой степени сухости пара и высоком давлении пользоваться упрощенным уравнением (5.5) нельзя, так как ошибка при этом может оказаться уже значительной. Практически это уравнение применяют к парам, имеющим степень сухости х не меньше 0,7.
Преобразуем уравнение (5.4), решив его относительно х:
vх = х v”+ (1 – х) v’ = х v”+ v’– х v’= х(v”– v’)+ v’,
откуда
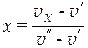 .
.
Обращаясь теперь к рис. 5.6, видим, что vх – v’ = bf, а v”– v’= bc.
Следовательно, графически
х = 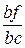 .
.
Для нахождения удельного объема перегретого пара было предложено в разное время несколько уравнений, дающих приближенные результаты. Наиболее точным из них является уравнение проф. М.П. Вукаловича и проф. И.И. Новикова, однако оно очень сложно. Поэтому удельные объемы перегретого пара обычно находят по специальным таблицам, о которых говорится в разделе VI.
Дата добавления: 2015-04-21; просмотров: 1287;
